Question

【题目】菱形的边长为，，、分别是、的中点，、分别在、上，且．

求证：四边形是平行四边形；

当四边形是菱形时，求的长；

当四边形是矩形时，求此时点到点的距离．

Answer 1

【答案】(1)详见解析；（2）1；（3）2.

【解析】

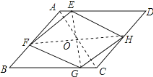
（1）根据菱形的性质结合已知条件易证△AEF≌△CGH，由全等三角形的性质可得EF=GH，继而求得BF=DH，BG=DE，同理可证△BGF≌△DEH，即可得GF=EH，根据两组对边相等的四边形为平行四边形即可得四边形EFGH是平行四边形；（2）如图，若为菱形，

只需要过且垂直，即，再求得及，根据30°角直角三角形的性质即可求得的长；（3）若是矩形只需要对角线相等，即，

只需与是所在边中点即可，所以；即点到点的距离为．

证明：∵四边形是菱形，

∴，，，

∵，分别是，的中点，

∴，

在与中，，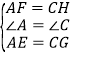

∴，

∴，

∵，

∴，，

同理证得，

∴，

∴四边形是平行四边形；

（2）如图，若为菱形，

只需要过且垂直，即，

∵是等边三角形，

∴，

∴，

∵，则，

∴

如图，若是矩形

只需要对角线相等，即，

只需与是所在边中点即可，

∴；

即点到点的距离为．