ЬтФПФкШн
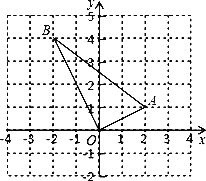
ЁОЬтФПЁПЖЈвхЃКШчЭМЂйЃЌХзЮяЯпyЃНax2ЃЋbxЃЋc(aЁй0)гыxжсНЛгкAЃЌBСНЕуЃЌЕуPдкИУХзЮяЯпЩЯ(PЕугыAЁЂBСНЕуВЛжиКЯ)ЃЎШчЙћЁїABPЕФШ§БпТњзуAP2ЃЋBP2ЃНAB2ЃЌдђГЦЕуPЮЊХзЮяЯпyЃНax2ЃЋbxЃЋc(aЁй0)ЕФЙДЙЩЕуЃЎ
(1)жБНгаДГіХзЮяЯпyЃНЃx2ЃЋ1ЕФЙДЙЩЕуЕФзјБъЃЎ
(2)ШчЭМЂкЃЌвбжЊХзЮяЯпyЃНax2ЃЋbx(aЁй0)гыxжсНЛгкAЃЌBСНЕуЃЌЕуP(1ЃЌ ![]() )ЪЧХзЮяЯпЕФЙДЙЩЕуЃЌЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЎ
)ЪЧХзЮяЯпЕФЙДЙЩЕуЃЌЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЎ
(3)дк(2)ЕФЬѕМўЯТЃЌЕуQдкХзЮяЯпЩЯЃЌЧѓТњзуЬѕМўSЁїABQЃНSЁїABPЕФQЕу(вьгкЕуP)ЕФзјБъЃЎ

ЁОД№АИЁП(1)(0ЃЌ1)(2) yЃН-![]() x(x-4)ЃН-
x(x-4)ЃН-![]() x2ЃЋ
x2ЃЋ![]() x(3)ТњзуЬѕМўЕФЕуQга3ИіЃЌЗжБ№ЮЊ(3ЃЌ
x(3)ТњзуЬѕМўЕФЕуQга3ИіЃЌЗжБ№ЮЊ(3ЃЌ ![]() )Лђ(2ЃЋ
)Лђ(2ЃЋ![]() ЃЌЃ
ЃЌЃ ![]() )Лђ(2Ѓ
)Лђ(2Ѓ![]() ЃЌЃ
ЃЌЃ ![]() )ЃЎ
)ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮі:(1)ИљОнХзЮяЯпЙДЙЩЕуЕФЖЈвхПЩвдЧѓНт,(2)зїPGЁЭxжс,гЩЕуPЕФзјБъЧѓЕУ:AG=1,PG=![]() ,гЩШ§НЧКЏЪ§ПЩЕУ:
,гЩШ§НЧКЏЪ§ПЩЕУ: ![]() ,ПЩжЊЁЯPAG=60ЁуДгЖјЧѓЕУAB=4,МДB(4,0),Д§ЖЈЯЕЪ§ЗЈПЩЧѓНтЕУ,(3)гЩ
,ПЩжЊЁЯPAG=60ЁуДгЖјЧѓЕУAB=4,МДB(4,0),Д§ЖЈЯЕЪ§ЗЈПЩЧѓНтЕУ,(3)гЩ![]() ЧвСНИіШ§НЧаЮЭЌЕз,ПЩжЊЕуQЕНxжсЕФОрРыЮЊ
ЧвСНИіШ§НЧаЮЭЌЕз,ПЩжЊЕуQЕНxжсЕФОрРыЮЊ![]() ,МДПЩЧѓНт.
,МДПЩЧѓНт.
(1)ХзЮяЯпyЃНЃx2ЃЋ1ЕФЙДЙЩЕуЕФзјБъЮЊ(0ЃЌ1)ЃЎ
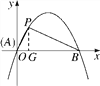
(2)ШчЭМЃЌзїPGЁЭxжсгкЕуG.ЁпЕуPЕФзјБъЮЊ(1ЃЌ![]() )ЃЌЁрAGЃН1ЃЌPGЃН
)ЃЌЁрAGЃН1ЃЌPGЃН![]() ЃЌЁрPAЃН
ЃЌЁрPAЃН![]() ЃН
ЃН![]() ЃН2.ЁпtanЁЯPABЃН
ЃН2.ЁпtanЁЯPABЃН![]() ЃН
ЃН![]() ЃЌЁрЁЯPAGЃН60Ёу.дкRtЁїPABжаЃЌABЃН
ЃЌЁрЁЯPAGЃН60Ёу.дкRtЁїPABжаЃЌABЃН![]() ЃН
ЃН![]() ЃН4ЃЌЁрЕуBЕФзјБъЮЊ(4ЃЌ0)ЃЎ
ЃН4ЃЌЁрЕуBЕФзјБъЮЊ(4ЃЌ0)ЃЎ
ЩшyЃНax(xЃ4)ЃЌНЋЕуP(1ЃЌ![]() )ДњШыЕУaЃНЃ
)ДњШыЕУaЃНЃ![]() ЃЌЁрyЃНЃ
ЃЌЁрyЃНЃ![]() x(xЃ4)ЃНЃ
x(xЃ4)ЃНЃ![]() x2ЃЋ
x2ЃЋ![]() x.
x.
(3)ЂйЕБЕуQдкxжсЩЯЗНЪБЃЌгЩSЁїABQЃНSЁїABPжЊЕуQЕФзнзјБъЮЊ![]() ЃЌдђгаЃ
ЃЌдђгаЃ![]() x2ЃЋ
x2ЃЋ![]() xЃН
xЃН![]() ЃЌНтЕУx1ЃН3ЃЌx2ЃН1(ВЛЗћКЯЬтвтЃЌЩсШЅ)ЃЌЁрЕуQЕФзјБъЮЊ(3ЃЌ
ЃЌНтЕУx1ЃН3ЃЌx2ЃН1(ВЛЗћКЯЬтвтЃЌЩсШЅ)ЃЌЁрЕуQЕФзјБъЮЊ(3ЃЌ![]() )ЃЎ
)ЃЎ
ЂкЕБЕуQдкxжсЯТЗНЪБЃЌгЩSЁїABQЃНSЁїABPжЊЕуQЕФзнзјБъЮЊЃ![]() ЃЌдђгаЃ
ЃЌдђгаЃ![]() x2ЃЋ
x2ЃЋ![]() xЃНЃ
xЃНЃ![]() ЃЌНтЕУx1ЃН2ЃЋ
ЃЌНтЕУx1ЃН2ЃЋ![]() ЃЌx2ЃН2Ѓ
ЃЌx2ЃН2Ѓ![]() ЃЌЁрЕуQЕФзјБъЮЊ(2ЃЋ
ЃЌЁрЕуQЕФзјБъЮЊ(2ЃЋ![]() ЃЌЃ
ЃЌЃ![]() )Лђ(2Ѓ
)Лђ(2Ѓ![]() ЃЌЃ
ЃЌЃ![]() )ЃЎ
)ЃЎ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуQга3ИіЃЌЗжБ№ЮЊ(3ЃЌ![]() )Лђ(2ЃЋ
)Лђ(2ЃЋ![]() ЃЌЃ
ЃЌЃ![]() )Лђ(2Ѓ
)Лђ(2Ѓ![]() ЃЌЃ
ЃЌЃ![]() )ЃЎ
)ЃЎ

 вЛХЕЪщвЕЪюМйзївЕПьРжМйЦкдЦФЯУРЪѕГіАцЩчЯЕСаД№АИ
вЛХЕЪщвЕЪюМйзївЕПьРжМйЦкдЦФЯУРЪѕГіАцЩчЯЕСаД№АИЁОЬтФПЁПЦЙХвЧђЪЧЮвЙњЕФЙњЧђЃЌвВЪЧЪРНчЩЯСїааЕФЧђРрЬхг§ЯюФП.ЮвЙњЦЙХвЧђУћНЋгыЦфЖдгІЩэИпШчЯТБэЫљЪОЃК
ЦЙХвЧђУћНЋ | СѕЪЋіЉ | ЕЫбЧЦМ | Азбю | ЖЁФў | ГТУЮ | ЫягБЩЏ | вІбх |
ЩэИпЃЈ | 160 | 155 | 171 | 173 | 163 | 160 | 175 |
етаЉЦЙХвЧђУћНЋЩэИпЕФжаЮЛЪ§КЭжкЪ§ЪЧЃЈ ЃЉ
A.160ЃЌ163B.173ЃЌ175C.163ЃЌ160D.172ЃЌ160