Question

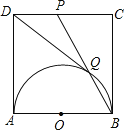
【题目】如图，正方形ABCD的边长为1，以AB为直径作半圆，点P是CD中点，BP与半圆交于点Q，连结DQ，给出如下结论：①；②；③；④，其中正确结论是______填写序号

Answer 1

【答案】①②④

【解析】

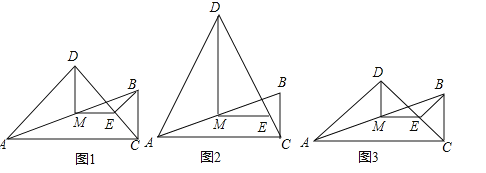
①连接OQ，OD，如图1．易证四边形DOBP是平行四边形，从而可得DO∥BP．结合OQ=OB，可证到∠AOD=∠QOD，从而证到△AOD≌△QOD，则有DQ=DA=1；
②连接AQ，如图2，根据勾股定理可求出BP．易证Rt△AQB∽Rt△BCP，运用相似三角形的性质可求出BQ，从而求出PQ的值，就可得到 的值；
③过点Q作QH⊥DC于H，如图3．易证△PHQ∽△PCB，运用相似三角形的性质可求出QH，从而可求出S△DPQ的值；
④过点Q作QN⊥AD于N，如图4．易得DP∥NQ∥AB，根据平行线分线段成比例可得，把AN=1-DN代入，即可求出DN，然后在Rt△DNQ中运用三角函数的定义，就可求出cos∠ADQ的值．

连接OQ，OD，如图1．

易证四边形DOBP是平行四边形，从而可得．

结合，可证到，从而证到≌，

则有．

故正确；

连接AQ，如图2．

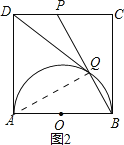
则有，．

易证∽，

运用相似三角形的性质可求得，

则，

．

故正确；

过点Q作于H，如图3．

易证∽，

运用相似三角形的性质可求得，

．

故错误；

过点Q作于N，如图4．

易得，

根据平行线分线段成比例可得，

则有，

解得：．

由，得．

故正确．

综上所述：正确结论是①②④．

故答案为：①②④．