题目内容
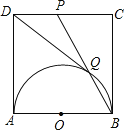
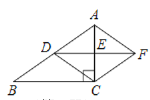
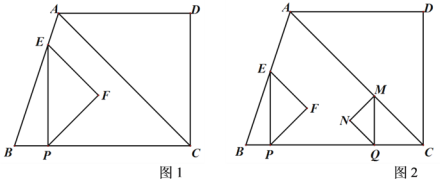
【题目】如图1,△ABC中,AC=![]() ,∠ACB=45°,tanB=3,过点A作BC的平行线,与过C且垂直于BC的直线交于点D,一个动点P从B出发,以每秒1个单位长度的速度沿BC方向运动,过点P作PE⊥BC,交折线BA-AD于点E,以PE为斜边向右作等腰直角三角形PEF,设点P的运动时间为t秒(t>0).
,∠ACB=45°,tanB=3,过点A作BC的平行线,与过C且垂直于BC的直线交于点D,一个动点P从B出发,以每秒1个单位长度的速度沿BC方向运动,过点P作PE⊥BC,交折线BA-AD于点E,以PE为斜边向右作等腰直角三角形PEF,设点P的运动时间为t秒(t>0).
(1)当点F恰好落在CD上时,此时t的值为 ;
(2)若P与C重合时运动结束,在整个运动过程中,设等腰直角三角形PEF与四边形ABCD重叠部分的面积为S,请求出S与t之间的函数关系式,并写出自变量t的取值范围;
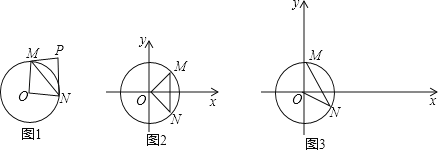
(3)如图2,在点P开始运动时,BC上另一点Q同时从点C出发,以每秒2个单位长度沿CB方向运动,当Q到达B点时停止运动,同时点P也停止运动,过Q作QM⊥BC交射线CA于点M,以QM为斜边向左作等腰直角三角形QMN,若点P运动到t秒时,两个等腰直角三角形分别有一条边恰好落在同一直线上,请直接写出t的值.
【答案】(1)7.5;(2)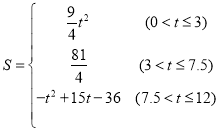 ;(3)2、4、
;(3)2、4、![]()
【解析】
(1)当点F落在CD上时,如图1所示,可知△DEF、△PCF均为等腰直角三角形,利用几何图形性质求出![]() 的长,进而 求出t的值;
的长,进而 求出t的值;
(2)点P的运动过程,可分为三种情形,在点P运动过程中: ①当0≤t<3时,如图2-1,利用锐角三角函数求解![]() 的长,直接利用面积公式写函数关系式,当3≤t<
的长,直接利用面积公式写函数关系式,当3≤t<![]() 时,如图2-2,利用三角函数求解
时,如图2-2,利用三角函数求解![]() 的长,直接利用面积公式写函数关系式,当
的长,直接利用面积公式写函数关系式,当![]() ≤t≤12时,如图2-3所示,利用等腰直角三角形的性质求解
≤t≤12时,如图2-3所示,利用等腰直角三角形的性质求解![]() 的长度,利用梯形面积公式写函数关系式;
的长度,利用梯形面积公式写函数关系式;
(3)点P、Q的运动过程,满足题意条件的有三种情形,①当EF与NQ落在同一直线上时,得△PEQ为等腰直角三角形,利用等腰三角形性质及![]() 的长列方程求解,如图3-1所示.当PF与MN落在同一直线上时,如图3-2所示,得△PQF为等腰直角三角形,利用等腰三角形性质及
的长列方程求解,如图3-1所示.当PF与MN落在同一直线上时,如图3-2所示,得△PQF为等腰直角三角形,利用等腰三角形性质及![]() 的长列方程求解,③当PE与QM落在同一直线上时,如图3-3所示,直接利用
的长列方程求解,③当PE与QM落在同一直线上时,如图3-3所示,直接利用![]() 长度列方程求解即可.
长度列方程求解即可.
解:(1)由题意可知,△ACD为等腰直角三角形,
∴AD=CD= ![]() =
= ![]()
如图1,过点A作AG⊥BC于点G,
则△ACG为等腰直角三角形.
∴AG=CG=![]() =
=![]()
在Rt△ABG中, tanB![]()
![]()
∴BC=BG+CG=3+9=12.
![]() 为等腰直角三角形,
为等腰直角三角形,![]()
![]() 当点F落在CD上时,△DEF、△PCF均为等腰直角三角形,
当点F落在CD上时,△DEF、△PCF均为等腰直角三角形,
∴DE=DF= ![]() EF,PC=CF=
EF,PC=CF=![]() PF.
PF.
∵△PEF为等腰直角三角形,EF=PF,
∴PC=CF=DF=![]() CD=
CD=![]() ,
,
∴BP=BC-PC=12-![]() =
=![]()
∴当点F恰好落在CD上时,t=![]() s.
s.
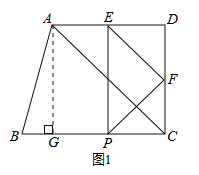
(2)在点P运动过程中: ①当0≤t<3时,如图2-1所示.
PE=BPtanB=3t, ![]()
S=![]()
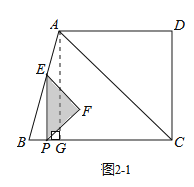
②当3≤t<![]() 时,如图2-2所示.
时,如图2-2所示.
S= ![]()
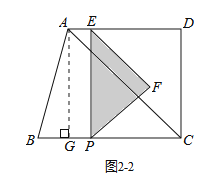
③当![]() ≤t≤12时,如图2-3所示.
≤t≤12时,如图2-3所示.
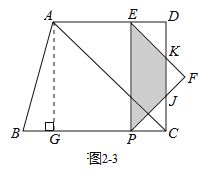
设EF、PF分别与CD交于点K、J,
同理可得△DEK、△PCJ均为等腰直角三角形,
∴DK=CJ=PC=12-t,
KJ=CD-DK-CJ=![]()
∴S=![]() (KJ+PE)PC=
(KJ+PE)PC=![]() (2t-15+9)(12-t)=
(2t-15+9)(12-t)=![]() .
.
综上所述,S与t之间的函数关系式为:
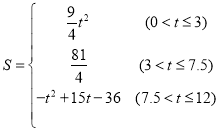
(3)在点P、Q的运动过程中:
①当EF与NQ落在同一直线上时,如图3-1所示.
此时,△PEQ为等腰直角三角形,则PQ=PE=3t.
∴BC=BP+PQ+CQ=t+3t+2t=12, ∴t= 2 s;
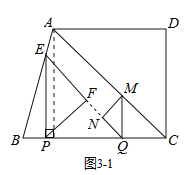
②当PF与MN落在同一直线上时,如图3-2所示.
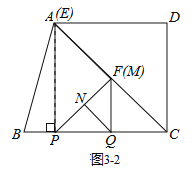
此时,△PQF为等腰直角三角形,则PQ=QF=CQ=2t.
∴BC=BP+PQ+CQ=t+2t+2t=12, ∴t=![]() s;
s;
③当PE与QM落在同一直线上时,如图3-3所示.
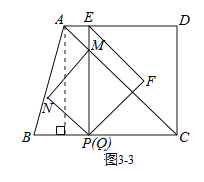
∴BC=BP+CQ=t+2t=12, ∴t=4 s.
综上所述,满足条件的t的值为:![]() 或
或![]() 或
或![]() .
.

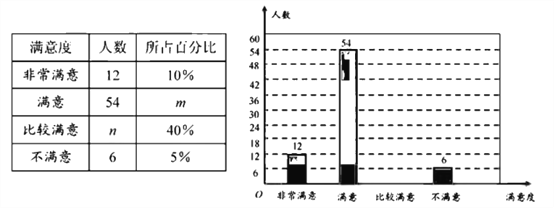
【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.收集数据:随机抽取甲乙两所学校的名学生的数学成绩进行
甲 91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙 84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理、描述数据:按如下数据段整理、描述这两组数据,分析数据:
分段 学校 |
|
|
|
|
|
|
|
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 |
两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 |
| 91 | 268.43 |
乙 | 81.95 | 86 | 88 | 115.25 |
(1)经统计,表格中![]() 的值是__________.
的值是__________.
(2)得出结论
①若甲学校有600名初二学生,估计这次考试成绩80分以上人数为__________.
②可以推断出__________学校学生的数学水平较高,理由为:__________.(至少从两个不同的角度说明推断的合理性)