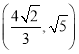题目内容
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A. 当m=﹣3时,函数图象的顶点坐标是(![]() ,
,![]() )
)
B. 当m>0时,函数图象截x轴所得的线段长度大于![]()
C. 当m≠0时,函数图象经过同一个点
D. 当m<0时,函数在x>![]() 时,y随x的增大而减小
时,y随x的增大而减小
【答案】D
【解析】分析:A、把m=-3代入[2m,1-m,-1-m],求得[a,b,c],求得解析式,利用顶点坐标公式解答即可;
B、令函数值为0,求得与x轴交点坐标,利用两点间距离公式解决问题;
C、首先求得对称轴,利用二次函数的性质解答即可;
D、根据特征数的特点,直接得出x的值,进一步验证即可解答.
详解:
因为函数y=ax2+bx+c的特征数为[2m,1﹣m,﹣1﹣m];
A、当m=﹣3时,y=﹣6x2+4x+2=﹣6(x﹣![]() )2+
)2+![]() ,顶点坐标是(
,顶点坐标是(![]() ,
,![]() );此结论正确;
);此结论正确;
B、当m>0时,令y=0,有2mx2+(1﹣m)x+(﹣1﹣m)=0,解得:x1=1,x2=﹣![]() ﹣
﹣![]() ,
,
|x2﹣x1|=![]() +
+![]() >
>![]() ,所以当m>0时,函数图象截x轴所得的线段长度大于
,所以当m>0时,函数图象截x轴所得的线段长度大于![]() ,此结论正确;
,此结论正确;
C、当x=1时,y=2mx2+(1﹣m)x+(﹣1﹣m)=2m+(1﹣m)+(﹣1﹣m)=0 即对任意m,函数图象都经过点(1,0)那么同样的:当m=0时,函数图象都经过同一个点(1,0),当m≠0时,函数图象经过同一个点(1,0),故当m≠0时,函数图象经过x轴上一个定点此结论正确.
D、当m<0时,y=2mx2+(1﹣m)x+(﹣1﹣m) 是一个开口向下的抛物线,其对称轴是:直线x=![]() ,在对称轴的右边y随x的增大而减小.因为当m<0时,
,在对称轴的右边y随x的增大而减小.因为当m<0时,![]() ,即对称轴在x=
,即对称轴在x=![]() 右边,因此函数在x=
右边,因此函数在x=![]() 右边先递增到对称轴位置,再递减,此结论错误;
右边先递增到对称轴位置,再递减,此结论错误;
根据上面的分析,①②③都是正确的,④是错误的.
故选:D.

 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
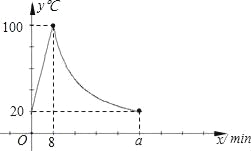
第三学期赢在暑假系列答案【题目】某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温和时间的关系如下图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的关系式;
(2)求出图中a的值;
(3)下表是该小学的作息时间,若同学们希望在上午第一节下课8:20时能喝到不超过40℃的开水,已知第一节下课前无人接水,请直接写出生活委员应该在什么时间或时间段接通饮水机电源.(不可以用上课时间接通饮水机电源)
时间 | 节次 | |
上 午 | 7:20 | 到校 |
7:45~8:20 | 第一节 | |
8:30~9:05 | 第二节 | |
… | … | |