题目内容
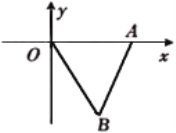
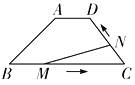
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,动点M从点B出发沿线段
,动点M从点B出发沿线段![]() 以每秒2个单位长度的速度向终点C运动;动点N同时从点C出发沿线段
以每秒2个单位长度的速度向终点C运动;动点N同时从点C出发沿线段![]() 以每秒1个单位长度的速度向终点D运动,设运动的时间为
以每秒1个单位长度的速度向终点D运动,设运动的时间为![]() .
.
(1)求![]() 的长.
的长.
(2)当![]() 时,求t的值
时,求t的值
(3)试探究:t为何值时,![]() 为等腰三角形?
为等腰三角形?
【答案】(1)10;(2)![]() ;(3)t=
;(3)t=![]() 、t=
、t=![]() 或t=
或t=![]() .
.
【解析】
(1)作梯形的两条高,根据直角三角形性质与矩形性质进一步求解即可;
(2)平移梯形的一腰,根据平行四边形的性质和相似三角形的性质进一步求解即可;
(3)因为三边中,每两条边都有相等的可能,所以考虑三种情况,结合路程=速度×时间求得其中有关的边,运用等腰三角形的性质和解直角三角形的方法进一步求解即可.
(1)
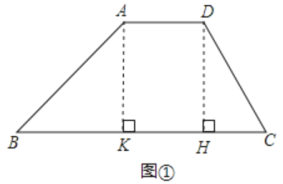
如图①,过A、D分别作AK⊥BC于K,作DH⊥BC于H,则四边形ADHK为矩形,
∴KH=AD=3,AK=DH,
在Rt△ABK中,
∴AK=ABsin45°=![]() =4,
=4,
又∵![]() ,
,
∴∠BAK=45°,
∴BK=AK=4,
∴DH=AK=4,
在Rt△CDH中,由勾股定理可得:
HC=![]() ,
,
∴BC=BK+KH+HC=4+3+3=10;
(2)
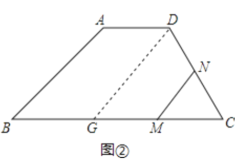
如图②,过D作DG∥AB交BC于G点,则四边形ADGB为平行四边形,
∴BG=AD=3,
∴GC=BCBC=103=7,
由题意得,当M、N运动t秒后,CN=t,CM=102t,
∵AB∥DG,MN∥AB,
∴DG∥MN,
∴∠NMC=∠DGC,
又∵∠C=∠C,
∴△MNC~△GDC,
∴![]() ,
,
∴![]() ,
,
解得t=![]() ;
;
(3)第一种情况:当NC=MC时,如图③,

此时t=102t,
∴t=![]() ;
;
第二种情况:当MN=NC时,如图④,作NE⊥MC于E,DH⊥BC于H,
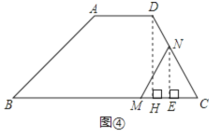
∵∠C=∠C,∠DHC=∠NEC=90°,
∴△NEC~△DHC,
∴![]() ,
,
即:![]() ,
,
解得:t=![]() ;
;
第三种情况:当MN=MC时,如图⑤,作DH⊥BC于H ,MF⊥CN于F,则FC=![]() ,
,

∵∠C=∠C,∠MFC=∠DHC=90°,
∴△MFC~△DHC,
∴![]() ,
,
即: ,
,
解得:t=![]() ;
;
综上所述,当t=![]() 、t=
、t=![]() 或t=
或t=![]() 时,△MNC为等腰三角形.
时,△MNC为等腰三角形.