Question

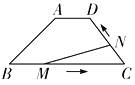
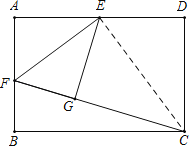
【题目】如图，矩形ABCD中，AB＝3，BC＝12，E为AD中点，F为AB上一点，将△AEF沿EF折叠后，点A恰好落到CF上的点G处，则折痕EF的长是_____．

Answer 1

【答案】

【解析】

由翻折知△AEF≌△GEF，进而证明△FEC∽△EDC，在利用三角形相似的性质可得到EF的长

如图，连接EC，

∵四边形ABCD为矩形，

∴∠A＝∠D＝90°，BC＝AD＝12，DC＝AB＝3，

∵E为AD中点，

∴AE＝DE＝AD＝6

由翻折知，△AEF≌△GEF，

∴AE＝GE＝6，∠AEF＝∠GEF，∠EGF＝∠EAF＝90°＝∠D，

∴GE＝DE，

∴EC平分∠DCG，

∴∠DCE＝∠GCE，

∵∠GEC＝90°﹣∠GCE，∠DEC＝90°﹣∠DCE，

∴∠GEC＝∠DEC，

∴∠FEC＝∠FEG+∠GEC＝×180°＝90°，

∴∠FEC＝∠D＝90°，

又∵∠DCE＝∠GCE，

∴△FEC∽△EDC，

∴，

∵EC＝，

∴，

∴FE＝2

故答案为：