题目内容
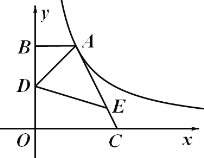
【题目】已知，
是
的直径，
，点
在的半径
上运动，
，垂足为，
，
为的切线，切点为
．
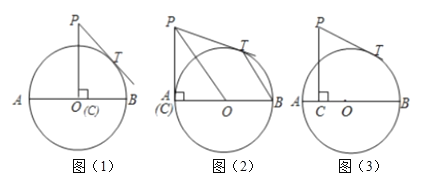
（1）如图（1），当点运动到
点时，求的长；
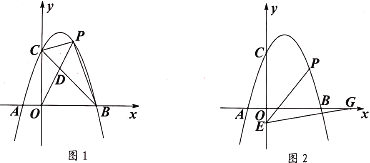
（2）如图（2），当点运动到
点时，连接
、
，求证：
；
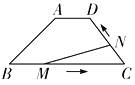
（3）如图（3），设
，
，求
与
的函数关系式及的最小值．
【答案】（1）3；（2）证明见解析；（3）
，
．
【解析】
（1）连接OT，根据题意，由勾股定理可得出PT的长；
（2）连接OT，则OP平分劣弧AT，则∠AOP=∠B，从而证出结论；
（3）设PC交⊙O于点D，延长线交⊙O于点E，由相交弦定理，可得出CD的长，再由切割线定理可得出y与x之间的关系式，进而求得y的最小值．
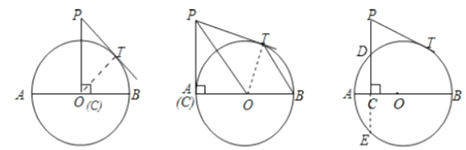
（1）连接
，
，
，
由勾股定理得：
；
（2）证明：连接，
，
为
的切线，
平分劣弧
，
，
，
，
；
（3）设交于点
，延长线交于点
，
由相交弦定理，得
，
，
，
，
由切割线定理，得
，
，
，
，
，
．
图（1） 图（2） 图（3）
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】一家蔬菜公司计划到某绿色蔬菜基地收购A，B两种蔬菜共140吨，预计两种蔬菜销售后获利的情况如下表所示：
销售品种 | A种蔬菜 | B种蔬菜 |
每吨获利(元) | 1200 | 1000 |
其中A种蔬菜的5%，B种蔬菜的3%须运往C市场销售，但C市场的销售总量不超过5.8吨．设销售利润为W元(不计损耗)，购进A种蔬菜x吨．
（1）求W与x之间的函数关系式；
（2）将这140吨蔬菜全部销售完，最多可获得多少利润？
（3）由于受市场因素影响，公司进货时调查发现，A种蔬菜每吨可多获利100元，B种蔬菜每吨可多获利m(200＜m＜400)元，但B种蔬菜销售数量不超过90吨．公司设计了一种获利最大的进货方案，销售完后可获利179000元，求m的值．
