题目内容
【题目】如图，一艘海轮位于灯塔P的南偏东60°方向，距离灯塔40海里的A处，它计划沿正北方向航行，去往位于灯塔P的北偏东45°方向上的B处．问B处距离灯塔P有多远？（结果精确到0.1海里） （参考数据： 
≈1.414， 
≈1.732， 
≈2.449）
【答案】解：作PH⊥AB于H， 在Rt△AHP中，sin∠PAH= 
，
∴PH=PAsin∠PAH=20 
，
在Rt△BPH中，sin∠B= 
∴PB= 
=20 
≈49.0，
答：B处距离灯塔P约为49.0海里．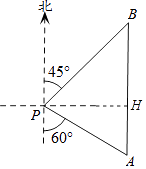
【解析】作PH⊥AB于H，根据正弦的定义求出PH，根据正弦的定义求出PB即可．
【考点精析】本题主要考查了关于方向角问题的相关知识点，需要掌握指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角才能正确解答此题．
练习册系列答案
相关题目
