��Ŀ����
����Ŀ�������龳��
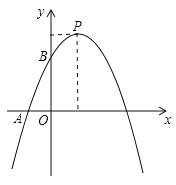
��ѧ����ϣ���ʦ��ͬѧ�����������ε���ת��Ϊ���չ��ѧ�����ABC�͡�DEC������ȫ�ȵ�ֱ��������ֽƬ�����С�ACB����DCE��90������B����E��30����AB��DE��4��
������⣺
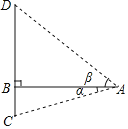
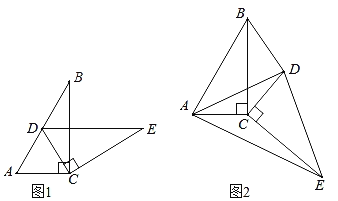
��1����ͼ1���ǻ�С�齫��DEC�Ƶ�C˳ʱ����ת�����ֵ���Dǡ������AB����ʱ��DE��AC�����������֤��������ۣ�
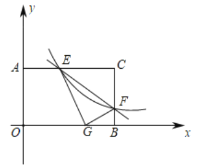
��2������С�����ǻ�С��Ļ����ϼ���̽��������DEC�Ƶ�C������ת����ͼ2��ʾ��λ��ʱ������AE��AD��BD���������S��BDC��S��AEC�������������֤��һ�����Ƿ���ȷ����˵�����ɣ�
���𰸡���1��֤������������2����ȷ�����ɼ�����
��������
��1����ͼ1�У�������ת�����ʿɵ�AC��CD��Ȼ�������ACD�ǵȱ������Σ����ݵȱ������ε����ʿɵá�ACD��60����Ȼ������ڴ�����ȣ���ֱ��ƽ�н��н��
��2����ͼ2�У���DM��BC��M��AN��EC��EC���ӳ�����N��������ת�����ʿɵ�BC��CE��AC��CD���������ACN����DCM��Ȼ���������ǽDZ���֤����ACN�͡�DCMȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�AN��DM��Ȼ�����õȵȸߵ������ε�������֤����
�⣺��1����ͼ1�У��ߡ�DEC�Ƶ�C��ת��Dǡ������AB���ϣ�
��AC��CD��
�ߡ�BAC��90������B��90����30����60����
���ACD�ǵȱ������Σ�
���ACD��60����
�֡ߡ�CDE����BAC��60����
���ACD����CDE��
��DE��AC��
��2��������ȷ��
�������£���ͼ2�У���DM��BC��M��AN��EC��EC���ӳ�����N��

�ߡ�DEC���ɡ�ABC�Ƶ�C��ת�õ���
��BC��CE��AC��CD��
�ߡ�ACN����BCN��90������DCM����BCN��180����90����90����
���ACN����DCM��
�ڡ�ACN�͡�DCM�У�
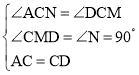 ��
��
���ACN�ա�DCM��AAS����
��AN��DM��
���BDC������͡�AEC�������ȣ��ȵȸߵ������ε������ȣ���
��S��BDC��S��AEC��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij�����깬ΪСѧ�������˻滭�����֡��赸����ȭ��������Ȥ�࣬Ϊ�˽�ѧ������������Ȥ���ϲ���������ѧ������������ʾ����飨�ʾ��������ͼ��ʾ�����������������������һ����������ͳ�Ʊ�
���ܻ�ӭ��Ȥ������ʾ� | ͳ�Ʊ� | |||||
ѡ�� | ��Ȥ�� | ��ѡ�� | ��Ȥ�� | Ƶ�� | Ƶ�� | |
A | �滭 | A | 0.35 | |||
B | ���� | B | 18 | 0.30 | ||
C | �赸 | C | 15 |
| ||
D | ��ȭ�� | D | 6 | |||
��ã���ѡ��һ����ֻ��ѡһ��������ϲ������Ȥ�࣬�����ո��ڴ�������лл��ĺ���. |
| 1 | ||||
�������ͳ�Ʊ����ṩ����Ϣ�ش��������⣺
��1��ͳ�Ʊ��е�![]() ��
��![]() ��
��
��2�����ݵ�������������Ƹ���2000��Сѧ������ϲ�����滭����Ȥ��������
��3����歺���Ҫѡ��μ���Ȥ�࣬������ÿ�˴�A��B��C��D������Ȥ�������ѡȡһ�࣬���û���״ͼ���б���ķ�����������ǡ��ѡ��ͬһ��ĸ��ʣ�