��Ŀ����
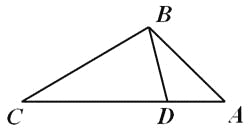
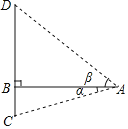
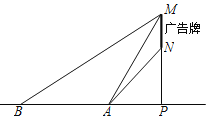
����Ŀ���¹ڷ��������ڼ䣬С��ͬѧ��������ѧ��֪ʶ�������Ҷ���ij����ƵĿ��ȣ�ͼ���߶�MN�ij�����ֱ��MN��ֱ�ڵ��棬����Ϊ��P���ڵ���A����õ�M������Ϊ58������N������Ϊ45������B����õ�M������Ϊ30����AB��5�ף���A��B��P������һֱ���ϣ�������������������ƵĿ�MN�ij������ο����ݣ�sin58��=0.85��cos58��=0.53��tan58��=1.60��![]() =1.73����
=1.73����
���𰸡�1.7��
��������
��Rt��APN�и�����֪�����õ�PA=PN����PA=PN=x���õ�MP=APtan��MAP=1.6x���������Ǻ����Ķ����з��̼��ɵõ����ۣ�
��Rt��APN����NAP��45����
��PA��PN��
��Rt��APM��tan��MAP��![]() ��
��
��PA��PN��x��
�ߡ�MAP��58����
��MP��APtan��MAP��1.6x��
��Rt��BPM��tan��MBP��![]() ��
��
�ߡ�MBP��30����AB��5��
��![]() ��
��
��x��2.82��
��MN��MP��NP��0.6x![]() 1.7���ף���
1.7���ף���
�𣺹���ƵĿ�MN�ij�Ϊ1.7�ף�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ