题目内容
【题目】如图,AB为⊙O直径,D为弧AC的中点,DG⊥AB于G,交AC于E,AC、BD相交于F.
(1)求证:AE=DE;
(2)若AG=2,DG=4,求AF的长.
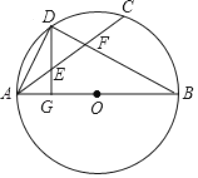
【答案】(1)见解析;(2)AF=5.
【解析】
(1)根据已知条件得到∠CAD=∠ABD,根据圆周角定理得到∠ADB=90°,根据余角的性质得到∠ADG=∠ABD,根据等腰三角形的判定定理即可得到结论;
(2)根据勾股定理得到AD= ![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
(1)∵D为![]() 的中点,
的中点,
∴![]() ,
,
∴∠CAD=∠ABD,
∵AB为⊙O直径,
∴∠ADB=90°,
∵DG⊥AB于G,
∴∠AGD=90°,
∴∠DAG+∠ABD=∠DAG+∠ADG=90°,
∴∠ADG=∠ABD,
∴∠ADG=∠DAE,
∴AE=DE;
(2)∵AG=2,DG=4,
∴AD=![]() ,
,
∵∠DAF=∠ADG,∠AGD=∠ADF,
∴△ADF∽△DGA,
∴![]() ,
,
∴AF=![]() =5.
=5.

练习册系列答案
相关题目
【题目】2018年12月4日是第五个国家宪法日,也是第一个“宪法宣传周”.甲、乙两班各选派10名学生参加宪法知识竞赛(满分100分),成绩如下:
成绩 | 85 | 90 | 95 | 100 |
甲班参赛学生/人 | 1 | 1 | 5 | 3 |
乙班参赛学生/人 | 1 | 2 | 3 | 4 |
分别求甲、乙两班参赛学生竞赛成绩的平均数和方差.