题目内容
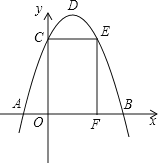
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于点A、B,与y轴交于点C,点O为坐标原点,点D为抛物线顶点,点E在抛物线上,点F在x轴上,四边形OCEF为矩形,且OF=2,EF=3,则△ABD的面积为_____.
【答案】8.
【解析】
利用矩形的性质得到E(2,3),C(0,3),再利用待定系数法求抛物线解析式,然后求出D点、A点、B点坐标,最后利用三角形面积公式计算.
∵四边形OCEF为矩形,且OF=2,EF=3,
∴E(2,3),C(0,3),
把E(2,3),C(0,3)代入y=﹣x2+bx+c得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3.
∵y=﹣x2+2x+3=-(x-1)2+4,
∴D(1,4),
令y=﹣x2+2x+3=0,解得:x1=-1,x2=3,
∴A(-1,0),B(3,0),
∴△ABD的面积=![]() ,
,
故答案为:8.

练习册系列答案
相关题目