题目内容
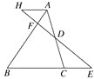
【题目】如图,△ABC中,D是AC的中点,E是BC延长线上一点,过A作AH∥BE,连接ED并延长交AB于F,交AH于H.
(1)求证:AH=CE;
(2)如果AB=4AF,EH=8,求DF的长.
【答案】(1)见解析;(2)2.
【解析】
(1)由于点D是AC的中点,AH∥CE,由平行线的性质知,可推出△ADH≌△CDE,故可得AH=CE;
(2)由平行线分对应线段成比例的性质知,AF∶AB=HF∶HE=1∶4,求得HF的值,由AH∥BE,D是AC的中点可得,点D也是EH的中点,求得HD的值,故有FD=HD-HF.
(1)证明 ∵AH∥BE,D是AC的中点,
∴△ADH≌△CDE,
∴AH=CE.
(2)解 ∵AB=4AF,AH∥BE,
∴AF∶AB=HF∶HE=1∶4,
∴HF=![]() EH=2,
EH=2,
∵AH∥BE,D是AC的中点,
∴点D也是EH的中点,即HD=![]() EH=4,
EH=4,
∴FD=HD-HF=2.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目