��Ŀ����
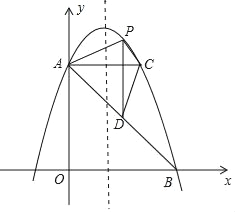
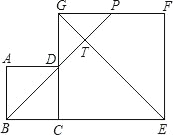
����Ŀ����ͼ��һ��Բ����ˮ�ص����봹ֱ��ˮ�氲װ��һ��������ˮװ��OA��Oǡ����ˮ�����ģ����������Ӷ���A������ͷ������ˮ��ˮ���ڸ�������������״��ͬ��������·�����£����ڹ�OA����һƽ���ϣ�����ͼ��ʾ����ֱ������ϵ��ˮ������ĸ߶�y(m)��ˮƽ����x(m)֮��Ĺ�ϵʽ������y����x2+bx+c��ʾ���������߾�����B(![]() ��2)��C(2��
��2)��C(2��![]() )�������������Ϣ������������⣻
)�������������Ϣ������������⣻
(1)�������ߵĺ�����ϵʽ����ȷ����ˮװ��OA�ĸ߶ȣ�
(2)�����ˮ����ˮ������߶��Ƕ����ף�
(3)�������������أ�ˮ�صİ뾶����Ҫ�����ף�����ʹ�����ˮ�����������ڳ��⣿

���𰸡�(1)y����x2+2x+![]() ����ˮװ��OA�ĸ߶���
����ˮװ��OA�ĸ߶���![]() �ף�(2)�����ˮ����ˮ������߶���
�ף�(2)�����ˮ����ˮ������߶���![]() �ף�(3)ˮ�صİ뾶����Ҫ2.5�ף�����ʹ�����ˮ�����������ڳ��⣮
�ף�(3)ˮ�صİ뾶����Ҫ2.5�ף�����ʹ�����ˮ�����������ڳ��⣮
��������
(1)���ݴ���ϵ������ֻ�轫B��C���������κ�������ʽ����������κ����Ľ���ʽ��
(2)���������ߵĶ��㣬����������ˮ������ˮ������߶ȣ�
(3)��������ֻ���ҵ���������x�ύ��ĺ����꣬����������ˮ������Զ���룬���ɵó���.
�⣺(1)��������y����x2+bx+c��ʾ���Ҿ�����B(![]() ��2)��C(2��
��2)��C(2��![]() )��
)��
��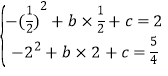 ��
��
��ã�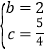 ��
��
��������y����x2+2x+![]() ��
��
��x��0ʱ��y��![]() ��
��
�������ߵĺ�����ϵʽ��y����x2+2x+![]() ����ˮװ��OA�ĸ߶���
����ˮװ��OA�ĸ߶���![]() �ף�
�ף�
(2)��y����x2+2x+![]() ����(x��1)2+
����(x��1)2+![]() ��
��
�൱x��1ʱ��yȡ�����ֵ����ʱy��![]() ��
��
�������ˮ����ˮ������߶���![]() �ף�
�ף�
(3)�x2+2x+![]() ��0��
��0��
��ã�x1����0.5��x2��2.5��
��ˮ�صİ뾶����Ҫ2.5�ף�����ʹ�����ˮ�����������ڳ��⣮

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�����Ŀ������Ϊ����ԭ��һ��¥����֣�ݻ�չ����(�׳ơ������ס�)�����ڷ羰�续�������������֣�ݹ۹���ο���Ӱ����Ѿ��㣮ѧ�������Ǻ���֪ʶ������������ͬѧ�������Լ�ѧ����֪ʶ�����������ס��ĸ߶ȣ������ƶ��˲��������������ÿ���ʱ�������ʵ�ز�����������Ŀ��������±���
��Ŀ | ���� | |||
���� | ����֣�ݻ�չ���ݵĸ߶� | |||
����ʾ��ͼ |
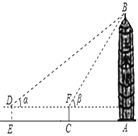
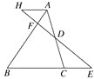
| ��ͼ����E���ò�����DE���¥��B������������ǰ��һ�ξ��뵽��C���ò�����CF���¥��B�������������ҵ�A��B��C��D��E��F����ͬһ��ֱƽ���� | ||
�������� | �����Ķ��� | �����Ķ��� | EC�ij��� | ������DE��CF�ĸ߶� |
40�� | 45�� | 53�� | 1.5�� | |
�� | �� | |||
���������С������ϱ��еIJ������ݣ����֣�ݻ�չ���ݵĸ߶�(�ο����ݣ�sin40���0.64��cos40���0.77��tan40���0.84�������������)