题目内容
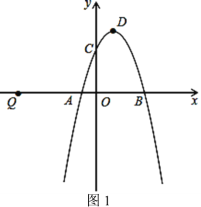
【题目】如图1,在平面直角坐标系中,抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
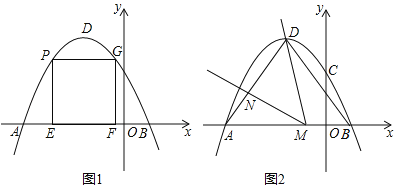
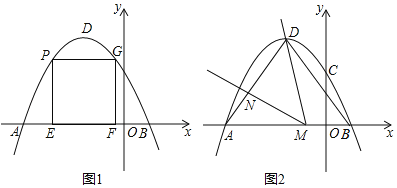
(1)求抛物线的解析式及顶点![]() 的坐标;
的坐标;
(2)点![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一点,过点
之间的一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,当矩形
,当矩形![]() 的周长最大时,求点
的周长最大时,求点![]() 的横坐标;
的横坐标;
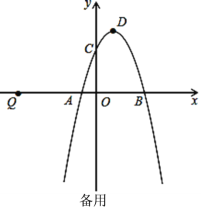
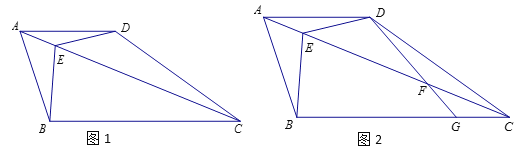
(3)如图2,连接![]() 、
、![]() ,点
,点![]() 在线段
在线段![]() 上(不与
上(不与![]() 、
、![]() 重合),作
重合),作![]() ,
,![]() 交线段
交线段![]() 于点
于点![]() ,是否存在这样点
,是否存在这样点![]() ,使得
,使得![]() 为等腰三角形?若存在,求出
为等腰三角形?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)![]() ;
;![]() ;(2)点
;(2)点![]() 的横坐标为
的横坐标为![]() ;(3)AN=1或
;(3)AN=1或![]() .
.
【解析】
(1)根据![]() 和点
和点![]() 可得抛物线的表达式为
可得抛物线的表达式为![]() ,可知对称轴为x=-2,代入解析式即可得出顶点坐标;(2)设点
,可知对称轴为x=-2,代入解析式即可得出顶点坐标;(2)设点![]() ,则
,则![]() ,
,![]() ,可得矩形
,可得矩形![]() 的周长
的周长![]() ,即可求解;(3)由D为顶点,A、B为抛物线与x轴的交点可得AD=BD,即可证明∠DAB=∠DBA,根据
,即可求解;(3)由D为顶点,A、B为抛物线与x轴的交点可得AD=BD,即可证明∠DAB=∠DBA,根据![]() ,利用角的和差关系可得
,利用角的和差关系可得![]() ,即可证明
,即可证明![]() ,可得
,可得![]() ;分
;分![]() 、
、![]() 、
、![]() ,三种情况分别求解即可.
,三种情况分别求解即可.
(1)∵抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
∴抛物线的表达式为:![]() ,
,
∴对称轴为:x=![]() =-2,
=-2,
把x=-2代入![]() 得:y=4,
得:y=4,
∴顶点![]() .
.
(2)设点![]() ,
,
则![]() ,
,![]() ,
,
矩形![]() 的周长
的周长![]()
![]() ,
,
∵![]() ,
,
∴当![]() 时,矩形
时,矩形![]() 周长最大,此时,点
周长最大,此时,点![]() 的横坐标为
的横坐标为![]() .
.
(3)∵点D为抛物线顶点,A、B为抛物线与x轴的交点,
∴AD=BD,
∴∠DAB=∠DBA,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵D(-2,4),A(-5,0),B(1,0)
∴![]() ,
,![]() ,
,
①当![]() 时,
时,
∵∠NAM=∠MBD,∠NMA=∠MBD,
∴![]() ,
,
∴![]() ,
,
∴![]() =AB-AM=1;
=AB-AM=1;
②当![]() 时,则
时,则![]() ,
,
∵∠DMN=∠DBA,
∴∠NDM=∠DBA,
∵∠DAB是公共角,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即:
,即:![]() ,
,
∴![]() ,
,
∵![]() ,即
,即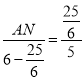 ,
,
∴![]() ;
;
③当![]() 时,
时,
∵![]() ,而
,而![]() ,
,
∴![]() ,
,
∴![]() ;
;
综上所述:![]() 或
或![]() .
.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】第二十四届冬季奥林匹克运动会将与2022年2月20日在北京举行,北京将成为历史上第一座举办过夏奥会又举办过冬奥会的城市,东宝区举办了一次冬奥会知识网上答题竞赛,甲、乙两校各有400名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
(收集数据)
从甲、乙两校各随机抽取20名学生,在这次竞赛中它们的成绩如下:
甲 | 30 | 60 | 60 | 70 | 60 | 80 | 30 | 90 | 100 | 60 |
60 | 100 | 80 | 60 | 70 | 60 | 60 | 90 | 60 | 60 | |
乙 | 80 | 90 | 40 | 60 | 80 | 80 | 90 | 40 | 80 | 50 |
80 | 70 | 70 | 70 | 70 | 60 | 80 | 50 | 80 | 80 |
(整理、描述数据)按如下分数段整理、描述这两组样本数据:
(说明:优秀成绩为80<x≤100,良好成绩为50<x≤80,合格成绩为30≤x≤50.)
学校 | 平均分 | 中位数 | 众数 |
甲 | 67 | 60 | 60 |
乙 | 70 | 75 | a |
30≤x≤50 | 50<x≤80 | 80<x≤100 | |
甲 | 2 | 14 | 4 |
乙 | 4 | 14 | 2 |
(分析数据)两组样本数据的平均分、中位数、众数如右表所示:其中a= .
(得出结论)
(1)小伟同学说:“这次竞赛我得了70分,在我们学校排名属中游略偏上!”由表中数据可知小明是 校的学生;(填“甲”或“乙”)
(2)老师从乙校随机抽取一名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为 ;
(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由.(至少从两个不同的角度说明推断的合理性)