题目内容
【题目】阅读下面材料，完成（1）﹣（3）题
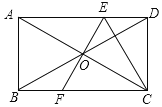
数学课上，老师出示了这样一道题：如图，四边形ABCD，AD∥BC，AB=AD，E为对角线AC上一点，∠BEC=∠BAD=2∠DEC，探究AB与BC的数量关系．
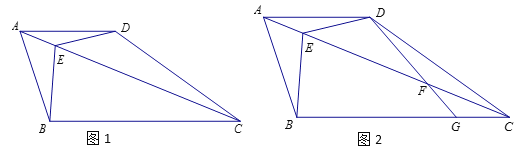
某学习小组的同学经过思考，交流了自己的想法：
小柏：“通过观察和度量，发现∠ACB=∠ABE”；
小源：“通过观察和度量，AE和BE存在一定的数量关系”；
小亮：“通过构造三角形全等，再经过进一步推理，就可以得到线段AB与BC的数量关系”．
……
老师：“保留原题条件，如图2， AC上存在点F，使DF=CF=
AE，连接DF并延长交BC于点G，求
的值”．
（1）求证：∠ACB=∠ABE；
（2）探究线段AB与BC的数量关系，并证明；
（3）若DF=CF=AE，求的值（用含k的代数式表示）．
【答案】（1）见解析；（2）CB=2AB；（3）
【解析】
（1）利用平行线的性质以及角的等量代换求证即可；
（2）在BE边上取点H，使BH=AE，可证明△ABH≌△DAE，△ABE∽△ACB，利用相似三角形的性质从而得出结论；
（3）连接BD交AC于点Q，过点A作AK⊥BD于点K，得出
，通过证明△ADK∽△DBC得出∠BDC=∠AKD=90°，再证DF=FQ，设AD=a，因此有DF=FC=QF=ka，再利用相似三角形的性质得出AC=3ka，
，
，从而得出答案．
解：（1）∵∠BAD=∠BEC
∠BAD=∠BAE+∠EAD
∠BEC=∠ABE+BAE
∴∠EAD=∠ABE
∵AD∥BC
∴∠EAD=∠ACB
∴∠ACB=∠ABE
（2）在BE边上取点H，使BH=AE
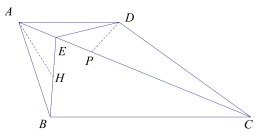
∵AB=AD
∴△ABH≌△DAE
∴∠AHB=∠AED
∵∠AHB+∠AHE=180°
∠AED+∠DEC=180°
∴∠AHE=∠DEC
∵∠BEC=2∠DEC
∠BEC=∠HAE+∠AHE
∴∠AHE=∠HAE
∴AE=EH
∴BE=2AE
∵∠ABE=∠ACB
∠BAE=∠CAB
∴△ABE∽△ACB
∴
∴CB=2AB；
（3）连接BD交AC于点Q，过点A作AK⊥BD于点K
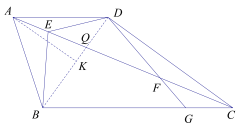
∵AD=AB
∴
∠AKD=90°
∵
∴
∵AD∥BC
∴∠ADK=∠DBC
∴△ADK∽△DBC
∴∠BDC=∠AKD=90°
∵DF=FC
∴∠FDC=∠DFC
∵∠BDC=90°
∴∠FDC+∠QDF=90°
∠DQF+∠DCF=90°
∴DF=FQ
设AD=a
∴DF=FC=QF=ka
∵AD∥BC
∴∠DAQ=∠QCB
∠ADQ=∠QBC
∴△AQD∽△CQB
∴
∴AQ=ka=QF=CF
∴AC=3ka
∵△ABE∽△ACB
∴
∴
同理△AFD∽△CFG
∴
．
阅读快车系列答案
