Question

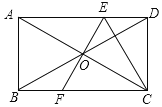
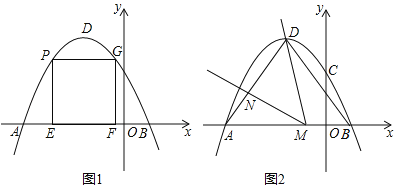
【题目】（探究）（1）如图①，点E、F、G、H分别在平行四边形ABCD的边AB、BC、CD、DA上，连结EF、FG、GH、HE，将△AEH、△BFE、△CGF、△DHG分别沿EF、FG、GH、HE折叠，折叠后的图形恰好能拼成一个无重叠、无缝隙的矩形．若，，求的长．

（拓展）（2）参考图②，四边形ABCD是平行四边形，，当按图①的方式折叠后的图形能拼成一个无重叠、无缝隙的正方形时，则___________．

Answer 1

【答案】（1）；（2）

【解析】

（1）根据题意可证△HGN≌△EFM，可得HN=FM，且AH=HM，可证AD=HF=5，根据勾股定理可求EH的长．

（2）由探究可得AD=HF，BE=EM=AE，∠B=∠EMF，由EFGH为正方形，可得HF=EF，∠EFH=45°，解△EFM可得EM=EF，则可求的值．

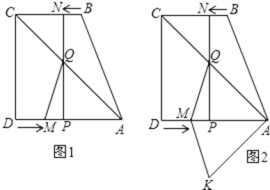
解：（1）如图1

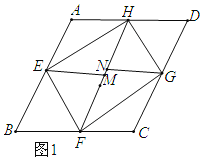
∵折叠后A、B落在点M处，C、D落在点N处．

∵四边形ABCD是平行四边形，

∴∠C+∠D=180°，∠B=∠D．

由折叠可知，

∠C=∠FNG，∠D=∠HNG，∠B=∠EMF=∠D=∠GNH，HD=HN，MF=BF，AH=MH．

∴H、N、F共线．

∵折叠后的图形恰好能拼成一个无重叠、无缝隙的矩形，

∴H、N、M、F共线，EF=HG，EF∥HG，∠FEH=90°．

∴∠NHG=∠MFE．

∴△EFM≌△GHN．

∴MF=BF=HN=HD．

∴AH+HD=MH+MF．

即AD=FH．

∵AD=5，EF=2，∠FEH=90°，

∴FH=5．

由勾股定理得

；

（2）如图2

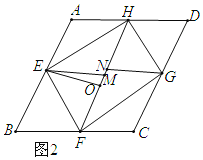
由探究可得：AD=HF，BE=EM=AE，∠B=∠EMF

∵∠A=120°，AD∥BC

∴∠B=60°=∠EMF

∵EHGF是正方形

∴EH=EF，∠EFH=45°

∴FH=EF

作EO⊥HF，且∠EFH=45°

∴EO=FO=EF

∵∠EMF=60°，EO⊥HF，

∴EO=OM，EM=2MO

∴OM=EF，EM=EF

∴BE=AE=EF

∴AB=EF

∴.

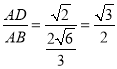故答案为：.