Question

【题目】在菱形ABCD中，∠A=60°，AB=4 ，点P在菱形内，若PB=PD=4，则∠PDC的度数为 ．

Answer 1

【答案】90°或30°
【解析】解：设AC和BE相交于点O． 当P在OA上时，
∵AB=AD，∠A=60°，
∴△ABD是等边三角形，
∴BD=AB=4 ，OB=OD= BD=2 ，∠ADO=60°，
∴cos∠PDO= = ，
∴∠PDO=30°，
∴∠ADP=60°﹣30°=30°，
∵四边形ABCD是菱形，
∴AB∥CD，
∴∠ADC=180°﹣60°=120°，
∴∠PDC=120°﹣30°=90°，
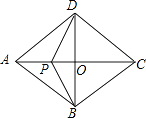
当P在OC上时，∵四边形ABCD是菱形，
∴∠DCB=∠DAB=60°，DC=BC，
∴△DBC是等边三角形，
∴∠BDC=60°，
∵∠PDO=30°，
∴∠PDC=30°，
所以答案是：90°或30°．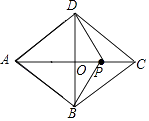


【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识，掌握等腰三角形的两个底角相等（简称：等边对等角），以及对菱形的性质的理解，了解菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．