题目内容
【题目】在△ABC中,AD⊥BC于点D,点E为AC边的中点,过点A作AF∥BC,交DE的延长线于点F,连接CF. 
(1)如图1,求证:四边形ADCF是矩形;
(2)如图2,当AB=AC时,取AB的中点G,连接DG、EG,在不添加任何辅助线和字母的条件下,请直接写出图中所有的平行四边形(不包括矩形ADCF).
【答案】
(1)证明:∵AF∥BC,
∴∠AFE=∠EDC,
∵E是AC中点,
∴AE=EC,
在△AEF和△CED中,
 ,
,
∴△AEF≌△CED,
∴EF=DE,∵AE=EC,
∴四边形ADCF是平行四边形,
∵AD⊥BC,
∴∠ADC=90°,
∴四边形ADCF是矩形
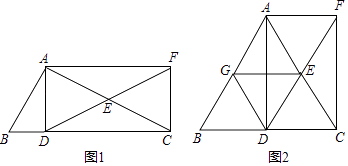
(2)∵线段DG、线段GE、线段DE都是△ABC的中位线,又AF∥BC,
∴AB∥DE,DG∥AC,EG∥BC,
∴四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形.
【解析】(1)由△AEF≌△CED,推出EF=DE,又AE=EC,推出四边形ADCF是平行四边形,只要证明∠ADC=90°,即可推出四边形ADCF是矩形.(2)四边形ABDF、四边形AGEF、四边形GBDE、四边形AGDE、四边形GDCE都是平行四边形.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目