题目内容
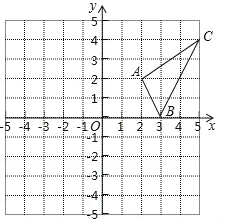
【题目】如图1,点![]() 的坐标为
的坐标为![]() ,将点
,将点![]() 向右平移
向右平移![]() 个单位得到点
个单位得到点![]() ,其中关于
,其中关于![]() 的一元一次不等式
的一元一次不等式![]() 的解集为
的解集为![]() ,过点
,过点![]() 作
作![]() 轴于
轴于![]() 得到长方形
得到长方形![]() ,
,
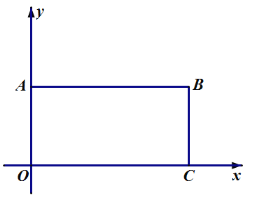
(1)求![]() 点坐标______及四边形
点坐标______及四边形![]() 的面积_______;
的面积_______;
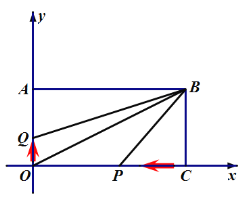
(2)如图2,点![]() 从
从![]() 点以每秒
点以每秒![]() 个单位长度的速度在
个单位长度的速度在![]() 轴上向上运动,同时点
轴上向上运动,同时点![]() 从
从![]() 点以每秒
点以每秒![]() 个单位长度的速度匀速在
个单位长度的速度匀速在![]() 轴上向左运动,设运动的时间为
轴上向左运动,设运动的时间为![]() 秒
秒![]() ,问是否存在一段时间,使得
,问是否存在一段时间,使得![]() 的面积不大于
的面积不大于![]() 的面积,若存在,求出
的面积,若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
(3)在(2)的条件下,四边形![]() 的面积是否发生变化,若不变化,请求出其值;若变化,说明理由.
的面积是否发生变化,若不变化,请求出其值;若变化,说明理由.
【答案】(1)![]() ;
;![]() ;(2)存在,
;(2)存在,![]() ;(3)不变;值为
;(3)不变;值为![]() .
.
【解析】
(1)利用不等式求出m的值,结合平移的性质得出B、C点坐标,再利用矩形面积求法得出答案;
(2)利用Q,P点移动速度分别表示出△BOQ和△BOP的面积,进而得出t的取值范围,即可得出答案;
(3)利用![]()
(1)由![]() 得,
得,![]()
∵不等式![]() 的解集为
的解集为![]()
∴![]()
解得m= 4
∵点A的坐标为(0, 2), 且向右平移b个单位得到点B
∴B(4, 2)
∵BC⊥x轴于C
∴C(4,0)
∵AB//OC,∠AOC=∠BCO = 90°
∴∠B+∠OCB = 180°
∴∠B=90°
∴四边形AOCB是矩形
∴![]()
故答案为:![]() ;
;![]() ;
;
(2)存在,理由如下:
由题意知: OQ= t,CP= 2t
∵四边形AOCB是矩形,OC= 4
∴∠BAO=∠BCO= 90°,OP=4- 2t
∴AB⊥OA,BC⊥OC
∵ ![]()
若![]() 的面积不大于
的面积不大于![]() 的面积.则
的面积.则![]()
解得:![]()
∵t>0
∴![]()
(3)不变,理由如下:
∵![]()
∴![]()
= 2t+4- 2t
=4

练习册系列答案
相关题目