题目内容
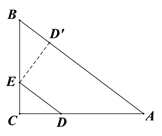
【题目】如图1,Rt△ABC中,∠C=90°,AB=15,BC=9,点D,E分别在AC,BC上,CD=4 x,CE=3x,其中0<x<3.
(1)求证:DE∥AB;
(2)当x=1时 ,求点E到AB的距离;
(3) 将△DCE绕点E逆时针方向旋转,使得点D落在AB边上的D′处. 在旋转的过程中,若点D′的位置有且只有一个,求x的取值范围.
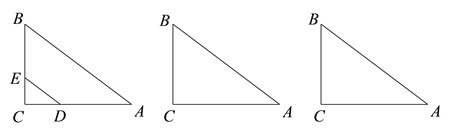
图1 备用图1 备用图2
【答案】(1)DE∥AB(2)![]() (3)
(3)![]() 或
或![]()
【解析】分析:(1)、根据线段之间的比值得出△CDE和△CAB相似,从而得出平行;(2)、过点E作EH⊥AB于点H,然后得出△BEH和△BAC相似得出EH的长度;(3)、本题分ED’⊥AB于点D’和D’与点B重合时两种情况分别求出x的值.
详解:(1)、∵![]() , ∴
, ∴![]() . ∵
. ∵![]() , ∴
, ∴![]() .
.
∵![]() ,∴
,∴![]() . ∴
. ∴![]() . ∴
. ∴![]() ∥
∥![]() .
.
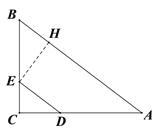
(2)、过点E作EH⊥AB于点H. ∵![]() ,∴
,∴![]() .
.
∵![]() , ∴
, ∴![]() .
.
∵![]() , ∴
, ∴![]() . ∴
. ∴![]() .
.
(3)、当ED’⊥AB于点D’,![]() , ∴
, ∴![]() . ∴
. ∴![]() .
.
当D’与点B重合时,![]() . ∴
. ∴![]() ,∴
,∴![]() .∴
.∴![]() .
.
综上:![]() 或
或![]() .
.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
【题目】某中学举行“校园好声音”歌手大赛,根据初赛成绩,初二和初三各选出5名选手组成初二代表队和初三代表队参加学校决赛。两个队各选出的5名选手的决赛成绩如图所示:
平均数(分) | 中位数(分) | 众数(分) | |
初二 | 85 | ||
初三 | 85 | 100 |
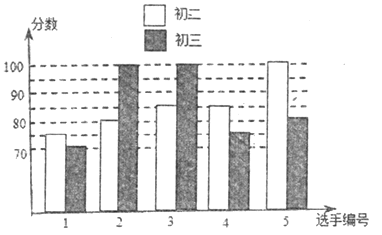
(1)根据图示填写上表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.