Question

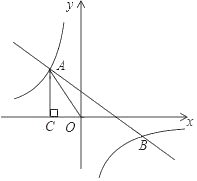
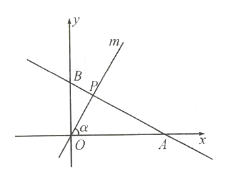
【题目】如图，已知在平面直角坐标系内，直线分别与轴、轴相交于点和点，直线为过点的旋转直线，交线段于点，直线与轴的正半轴的夹角为.

（1）当直线旋转到与线段垂直时，求的值；

（2）当直线旋转到过线段中点时，求的值.

Answer 1

【答案】（1）；（2）

【解析】

（1）分别求出点A和点B的坐标，从而得到OA，OB的长，再通过转化思想，=,从而问题得解；

（2）由AP=BP，∠AOB=90°，可得OP=PA，所以=,从问题得解.

解：令x=0,则y=3,即OB=3，

令y=0，则x=4,即OA=4,

(1)∵直线旋转到与线段垂直,

∴∠AOP+∠OAP=90°，

∵∠OBP+∠OAP=90°，

∴∠AOP=∠OBP

∴== =.

∴当直线旋转到与线段垂直时的值是.

(2)∵直线旋转到过线段中点，

∴OP=AP=BP.

∴∠AOP=∠BAO

∴== =.

∴当直线旋转到过线段中点时的值是.