题目内容
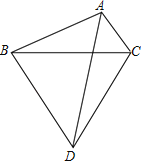
【题目】如图,在△ABC中,BD是AC边上的高,点E在边AB上,联结CE交BD于点O,且![]() ,AF是∠BAC的平分线,交BC于点F,交DE于点G.
,AF是∠BAC的平分线,交BC于点F,交DE于点G.
(1)求证:CE⊥AB.
(2)求证:![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)首先判定Rt△ADB∽Rt△ODC,得出∠ABD =∠OCD,然后通过三角形内角和转换得出∠OEB = 90°,进而得出CE⊥AB;
(2)首先判定△ADB∽△AEC,得出![]() ,然后再判定△DAE∽△BAC,得出
,然后再判定△DAE∽△BAC,得出![]() ,进而得出
,进而得出![]() .
.
(1)∵![]() ,
,
∴![]() .
.
∵BD是AC边上的高,
∴∠BDC = 90°,△ADB和△ODC是直角三角形.
∴Rt△ADB∽Rt△ODC.
∴∠ABD =∠OCD.
又∵∠EOB=∠DOC,∠DOC+∠OCD+∠ODC=180°,
∠EOB +∠ABD+∠OEB =180°.
∴∠OEB = 90°.
∴CE⊥AB.
(2)在△ADB和△AEC中,
∵∠BAD=∠CAE,∠ABD =∠OCD,
∴△ADB∽△AEC.
∴![]() , 即
, 即![]() .
.
在△DAE和△BAC中
∵∠DAE =∠BAC,![]() .
.
∴△DAE∽△BAC.
∵AF是∠BAC的平分线,
∴![]() ,即
,即![]() .
.

练习册系列答案
相关题目