题目内容
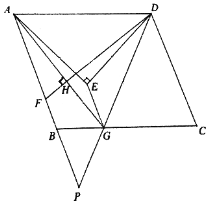
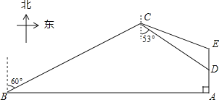
【题目】如图，一般捕鱼船在A处发出求救信号，位于A处正西方向的B处有一艘救援艇决定前去数援，但两船之间有大片暗礁，无法直线到达．救援艇决定马上调整方向，先向北偏东
方以每小时30海里的速度航行，同时捕鱼船向正北低速航行．30分钟后，捕鱼船到达距离A处
海里的D处，此时救援艇在C处测得D处在南偏东
的方向上．
求C、D两点的距离；
捕鱼船继续低速向北航行，救援艇决定再次调整航向，沿CE方向前去救援，并且捕鱼船和救援艇同达时到E处，若两船航速不变，求
的正弦值．
参考数据：
，
，
【答案】（1）CD两点的距离是10海里；（2）0.08
【解析】
过点C、D分别作
，
，垂足分别为G，F，根据直角三角形的性质得出CG，再根据三角函数的定义即可得出CD的长；
如图，设渔政船调整方向后t小时能与捕渔船相会合，由题意知
，
，
，过点E作
于点H，根据三角函数表示出EH，在
中，根据正弦的定义求值即可；
解：过点C、D分别作，，垂足分别为G，F，
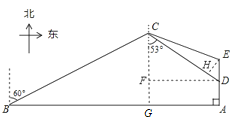
在
中，
，
海里，
，
四边形ADFG是矩形，
海里，
海里，
在
中，
，
，
，
海里
．
答：CD两点的距离是10海里；
如图，设渔船调整方向后t小时能与捕渔船相会合，
由题意知，，，
过点E作于点H，则
，
，
，
在中，
．
答：
的正弦值是
．
练习册系列答案
相关题目
