题目内容
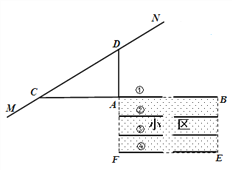
【题目】直线AB∥CD,EF分别交AB、CD于点M、N,NP平分∠MND. 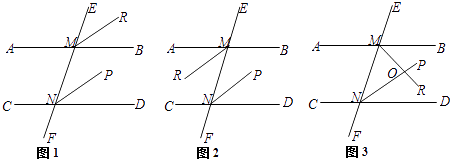
(1)如图1,若MR平分∠EMB,则MR∥NP.请你把下面的解答过程补充完整: 解:因为AB∥CD(已知)
所以∠EMB=∠END()
因为MR平分∠EMB,NP平分∠MND(已知)
所以∠EMR= ![]() ∠EMB,∠MNP=
∠EMB,∠MNP= ![]() ∠MND(角平分线定义)
∠MND(角平分线定义)
所以∠EMR=∠MNP
所以MR∥NP()
(2)如图2,若MR平分∠AMN,则MR与NP又怎样的位置关系?请在横线上写出你的猜想结论:;
(3)如图3,若MR平分∠BMN,则MR与NP又怎样的位置关系?请说明理由.
【答案】
(1)两直线平行,同位角相等;同位角相等,两直线平行
(2)MR∥NP
(3)解:MR⊥NP;理由如下:
因为AB∥CD,
所以∠BMN+∠MND=180°,
因为MR平分∠BMN,NP平分∠MND,
所以∠RMN= ![]() ∠BMN,∠MNP=
∠BMN,∠MNP= ![]() ∠MND,
∠MND,
所以∠RMN+∠MNP= ![]() (∠BMN+∠MND)=90°,
(∠BMN+∠MND)=90°,
所以∠MON=90°,
所以MR⊥NP
【解析】解:(1)因为AB∥CD(已知)所以∠EMB=∠END(两直线平行,同位角相等)因为MR平分∠EMB,NP平分∠MND(已知)所以∠EMR= ![]() ∠EMB,∠MNP=
∠EMB,∠MNP= ![]() ∠MND(角平分线定义)所以∠EMR=∠MNP所以MR∥NP(同位角相等,两直线平行)所以答案是:两直线平行,同位角相等;同位角相等,两直线平行; (2)MR∥NP;理由如下:因为AB∥CD(已知)所以∠AMN=∠MND(两直线平行,内错角相等)因为MR平分∠AMN,NP平分∠MND(已知)所以∠NMR=
∠MND(角平分线定义)所以∠EMR=∠MNP所以MR∥NP(同位角相等,两直线平行)所以答案是:两直线平行,同位角相等;同位角相等,两直线平行; (2)MR∥NP;理由如下:因为AB∥CD(已知)所以∠AMN=∠MND(两直线平行,内错角相等)因为MR平分∠AMN,NP平分∠MND(已知)所以∠NMR= ![]() ∠AMN,∠MNP=
∠AMN,∠MNP= ![]() ∠MND(角平分线定义)所以∠NMR=∠MNP所以MR∥NP(内错角相等,两直线平行)所以答案是:MR∥NP;
∠MND(角平分线定义)所以∠NMR=∠MNP所以MR∥NP(内错角相等,两直线平行)所以答案是:MR∥NP;
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

 阅读快车系列答案
阅读快车系列答案