��Ŀ����
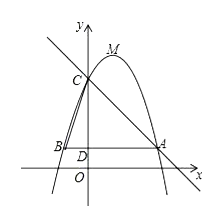
����Ŀ����ͼ����֪���κ���y=��x2+bx+c��b��cΪ��������ͼ����A��5��3������C��0��8��������Ϊ��M������A��AB��x�ᣬ��y���ڵ�D�����ö��κ���ͼ���ڵ�B������BC��
��1����ö��κ����Ľ���ʽ����M�����ꣻ
��2������ABC�������
��3�������ö��κ���ͼ������ƽ��m��m��0������λ��ʹƽ�ƺ�õ��Ķ��κ���ͼ��Ķ���������ABC���ڲ�����������ABC�ı߽磩����m��ȡֵ��Χ��

���𰸡���1��y=����x��2��2+12��M��2��12��
��2��S��ABC=15
��3��6��m��9
��������
�����������1���ѵ�A��C��������뺯������ʽ���ô���ϵ������������߽���ʽ��
��2����ϵ�A��B��C�����꣬�����ε������ʽ���н��
��3����M�����ŶԳ���ֱ��x=2����ƽ�Ƶģ��������ֱ��AC�Ľ���ʽ����x=2���������M������ƽ��ʱ��AC��AB�ཻʱy��ֵ�����ɵõ�m��ȡֵ��Χ��
�⣺��1���ѵ�A��5��3������C��0��8��������κ���y=��x2+bx+c����
![]() ��
��
���![]() ��
��
�����κ�������ʽΪy=��x2+4x+8���䷽��y=����x��2��2+12
����M��������2��12����
��2���ɣ�1��֪�������ߵĶԳ�����x=2��
��A��5��3����AB��x�ᣬ
��AB=6��D��0��3��
��C��0��8����
��CD=5��
���ABC�����=![]() ABCD=
ABCD=![]() ��6��5=15��
��6��5=15��
����ABC�����=15��
��3����ֱ��AC����ʽΪy=kx+b���ѵ�A��5��3����C��0��8������![]() ��
��
���![]() ��
��
��ֱ��AC�Ľ���ʽΪy=��x+8���Գ���ֱ��x=2����ABC���߷ֱ��ڵ�E����F��
��x=2����ֱ��AC����ʽy=��x+8��
���y=6�����E������2��6������F������2��3��
��3��12��m��6�����6��m��9��