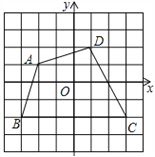
[题目] 如图.已知四边形ABCD(网格中每个小正方形的边长均为1)．(1)写出点A.B.C.D的坐标,(2)求四边形ABCD的面积．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，已知四边形ABCD（网格中每个小正方形的边长均为1）．

（1）写出点A，B，C，D的坐标；

（2）求四边形ABCD的面积．

【答案】（1）A（﹣2，1），B（﹣3，﹣2），C（3，﹣2），D（1，2）；（2）16．

【解析】试题分析:(1)利用平面直角坐标系点的坐标含义和特征可得: A（﹣2,1）,

B（﹣3,﹣2）,C（3,﹣2）,D（1,2）,(2)利用割补法求图形面积,先在四边形ABCD的内部将四边形分割成三个直角三角形和一个正方形,然后分别计算三角形和正方形的面积,再求和.

试题解析:（1）由图象可知A（﹣2,1）,B（﹣3,﹣2）,C（3,﹣2）,D（1,2）,

（2）S四边形ABCD=S△ABE+S△ADF+S△CDG+S正方形AEGF= ×1×3+ ×1×3+ ×2×4+3×3=16．

练习册系列答案

中考分类必备全国中考真题分类汇编系列答案

【题目】若x= -2是关于x的方程2x-3m﹣2=0的解，则m的值为________.

【题目】直线AB∥CD，EF分别交AB、CD于点M、N，NP平分∠MND．
（1）如图1，若MR平分∠EMB，则MR∥NP．请你把下面的解答过程补充完整：解：因为AB∥CD（已知）
所以∠EMB=∠END（）
因为MR平分∠EMB，NP平分∠MND（已知）
所以∠EMR= ∠EMB，∠MNP= ∠MND（角平分线定义）
所以∠EMR=∠MNP
所以MR∥NP（）
（2）如图2，若MR平分∠AMN，则MR与NP又怎样的位置关系？请在横线上写出你的猜想结论：；
（3）如图3，若MR平分∠BMN，则MR与NP又怎样的位置关系？请说明理由．

【题目】如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，联结AD，以AD为一边且在AD的右侧作正方形ADEF．

（1）如果AB=AC，∠BAC=90°，

①当点D在线段BC上时（与点B不重合），如图2，将△ABD绕A点逆时针旋转90°，所得到的三角形为，线段CF、BD所在直线的位置关系为，线段CF、BD的数量关系为；

②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；

（2）如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足什么条件时，CF⊥BC（点C、F不重合），并说明理由．

【题目】已知Rt△ABC中，∠A=90°，∠B=50°，则∠C=_________°.

【题目】画图并填空：如图，方格纸中每个小正方形的边长都为1．在方格纸内将△ABC经过一次平移后得到△A′B′C′，图中标出了点B的对应点B′．
（1）在给定方格纸中画出平移后的△A′B′C′；画出AB边上的中线CD；画出BC边上的高线AE；
（2）△A′B′C′的面积为．

【题目】已知点A（1，0），B（0，2），点P在x轴上，且△PAB的面积为5，则点P的坐标是（）
A.（﹣4，0）
B.（6，0）
C.（﹣4，0）或（6，0）
D.（0，12）或（0，﹣8）

【题目】在平面直角坐标系中，点P（﹣2，3）向右平移3个单位长度后的坐标为（）
A.（3，6）
B.（1，3）
C.（1，6）
D.（6，6）

试题分类