题目内容
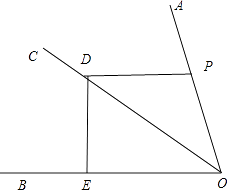
【题目】如图所示,OC为∠AOB的角平分线, 
(1)作图: ①在OA边上任取一点P,过点P作PD∥OB,交OC于点D;
②过点D作DE⊥OB,垂足为点E.
(2)求∠PDE的度数.
(3)若∠PDO=40°,求∠AOB的度数.
【答案】
(1)解:如图,
(2)解:∵DE⊥OB,
∴∠DEO=90°,
∵PD∥OB,
∴∠PDE+∠DEO=180°,
∴∠PDE=180°﹣∠DEO=180°﹣90°=90°
(3)解:∵PD∥OB,
∴∠PDO=∠DOE,
∵∠PDO=40°,
∴∠DOE=40°,
∵OC平分∠AOB,
∴∠AOB=2∠DOE=80°
【解析】(1)利用题中几何语言画图;(2)先根据垂直的定义得到∠DEO=90°,然后根据平行线的性质计算∠PDE的度数;(3)先根据平行线的性质得到∠PDO=∠DOE=40°,然后根据角平分线的定义计算∠AOB的度数.
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补).

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
【题目】某专卖店专营某品牌的鞋,店主对上一周中不同号码的鞋销售情况统计如下:
号码 | 39 | 40 | 41 | 42 | 43 |
平均每天销售数量/件 | 10 | 12 | 20 | 12 | 12 |
该店主决定本周进货时,增加了一些41号码的鞋,影响该店主决策的统计量是( )
A.众数B.方差C.平均数D.中位数