题目内容
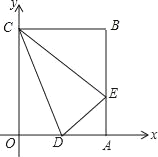
【题目】如图,在平面直角坐标系中,已知点A(10,0),B(4,8),C(0,8),连接AB,BC,点P在x轴上,从原点O出发,以每秒1个单位长度的速度向点A运动,同时点M从点A出发,以每秒2个单位长度的速度沿折线A﹣B﹣C向点C运动,其中一点到达终点时,另一点也随之停止运动,设P,M两点运动的时间为t秒.
(1)求AB长;
(2)设△PAM的面积为S,当0≤t≤5时,求S与t的函数关系式,并指出S取最大值时,点P的位置;
(3)t为何值时,△APM为直角三角形?
【答案】(1)10;(2)中点处;(3)![]() 或
或![]() .
.
【解析】试题分析:(1)过点![]() 作
作![]() 轴于点
轴于点![]() ,利用勾股定理求出
,利用勾股定理求出![]() 的长度;
的长度;
(2)先判断出点![]() 在
在![]() 上,然后表示出
上,然后表示出![]() 即可用三角形的面积公式即可;
即可用三角形的面积公式即可;
(3)![]() 为直角三角形时,由于没有规定哪个顶点是直角顶点,所以分三种情况进行讨论;利用锐角三角函数或相似三角形的性质即可.
为直角三角形时,由于没有规定哪个顶点是直角顶点,所以分三种情况进行讨论;利用锐角三角函数或相似三角形的性质即可.
试题解析:
(1)如图1,过点B作BD⊥x轴于点D,
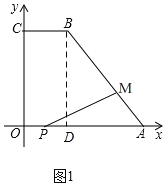
∵A(10,0),B(4,8)C(0,8),
∴AO=10,BD=8,AD=6,
由勾股定理可求得:AB=10,
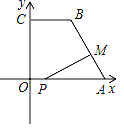
(2)∵AB=10,
∴10÷2=5,
![]()
∴点M在AB上,
作ME⊥OA于E,
∴△AEM∽△ADB,
![]()
![]()
![]()
![]()
![]()
∴t=5时,S取最大值,此时PA=10t=5,
即:点P在OA的中点处.
(3)由题意可知:![]()
当点P是直角顶点时,
∴PM⊥AP,
∴PA=10t,
若![]() 时,点M在AB上,如图2,
时,点M在AB上,如图2,
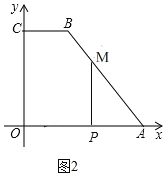
此时AM=2t,
![]()
![]()
![]()
若![]() 时,点M在BC上,如图3,
时,点M在BC上,如图3,
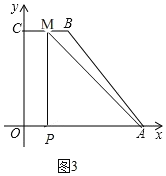
∴CM=142t,OP=t,
∴OP=CM,
∴t=142t,
![]() 当点A是直角顶点时,
当点A是直角顶点时,
此时,∠MAP不可能为![]() 此情况不符合题意;
此情况不符合题意;
当点M是直角顶点时,
若![]() 时,M在AB上,如图4,
时,M在AB上,如图4,
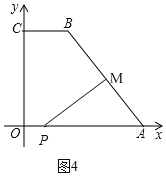
此时,AM=2t,AP=10t
![]()
![]()
![]()
![]()
若![]() 时,点M在BC上,如图5,
时,点M在BC上,如图5,
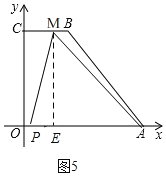
过点M作ME⊥x轴于点E,
此时,CM=142t,OP=t,
∴ME=8,PE=CMOP=143t,
∴EA=10(142t)=2t4,
![]()
![]()
∴∠PME=∠MAP,
∴△PME∽△MAE,
![]()
![]()
∴64=(143t)(2t4),
![]()
![]() 故此情况不存在;
故此情况不存在;
综上所述,t=![]() 或
或![]()

 阅读快车系列答案
阅读快车系列答案