题目内容
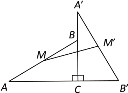
【题目】如图,在Rt△ABC中,∠C=90°,将△ABC绕点C顺时针旋转90°得到△A′B′C,M、M′分别是AB、A′B′的中点,若AC=8,BC=6,则线段MM′的长为____.
【答案】![]()
【解析】
先利用勾股定理求出AB的长,根据直角三角形斜边上的中线等于斜边的一半的性质求出CM=![]() AB,然后连接CM、CM′,再根据旋转的性质求出∠MCM′=90°,CM=CM′,再利用勾股定理列式求解即可.
AB,然后连接CM、CM′,再根据旋转的性质求出∠MCM′=90°,CM=CM′,再利用勾股定理列式求解即可.
连接CM,CM′,

∵AC=8,BC=6,
∴AB= ![]() =10,
=10,
∵M是AB的中点,
∴CM=![]() AB=5,
AB=5,
∵Rt△ABC绕点C顺时针旋转90°得到Rt△A′B′C,
∴∠A′CM′=∠ACM
∵∠ACM+∠MCB=90°,
∴∠MCB+∠BCM′=90°,
又∵CM=C′M′,
∴△CMM′是等腰直角三角形,
∴MM′=![]() CM=5
CM=5![]() ,
,
故答案为:5![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目