题目内容
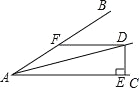
【题目】如图∠BAC=30°,D 为角平分线上一点,DE⊥AC 于 E,DF∥AC且交AB于F.
(1)求证:△ADF 是等腰三角形.
(2)若 DF=10cm,求 DE的长.
【答案】(1)证明见解析;(2)5cm.
【解析】
(1)根据角平分线的定义、平行线的性质、等腰三角形的判定定理证明;
(2)作DH⊥AB于H,根据直角三角形的性质求出BH,根据角平分线的性质定理解答.
(1)证明:∵∠BAC=30°,D为角平分线上一点,
∴∠BAD=∠CAD,
∵DF∥AC,
∴∠CAD=∠FDA,
∴∠BAD=∠FDA,
∴FA=FD,即△ADF是等腰三角形;
(2)解:作DH⊥AB于H,
∵DF∥AC,
∴∠BFD=∠BAC=30°,
∴DH=![]() DF=5,
DF=5,
∵D为角平分线上一点,DE⊥AC,DH⊥AB,
∴DE=DH=5cm.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
【题目】去年6月某日自治区部分市、县的最高气温(℃)如下表:
区县 | 吐鲁番 | 塔城 | 和田 | 伊宁 | 库尔勒 | 阿克苏 | 昌吉 | 呼图壁 | 鄯善 | 哈密 |
气温(℃) | 33 | 32 | 32 | 30 | 30 | 29 | 29 | 31 | 30 | 28 |
则这10个市、县该日最高气温的众数和中位数分别是( )
A.32,32
B.32,30
C.30,30
D.30,32