题目内容
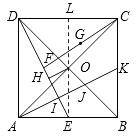
【题目】如图，正方形ABCD的边长为2，对角线AC与BC相交于O ， E为AB的中点，F为DE的中点，G为CF的中点， OH⊥DE于H ， 过A作AI⊥DE于I ， 交BD于J ， 交BC于K ， 连接BI ．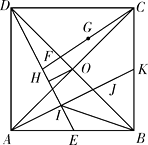 
下列结论：①G到AC的距离等于 
；②OH＝ 
；③BK＝ 
AK；④∠BIJ＝45°．其中正确的结论是
A.①②③
B.①②④
C.①③④
D.①②③④
【答案】B
【解析】解：①正确，链接AF、AG，
则S△AFC=S△ADC-S△CDF=2-
×2×-×2×1=
∵S△AFC=2S△AGC ， 所∴S△AGC=
设G到AG的距离为h，则由AC
h=
由勾股定理AC=
=2
，
∴h=
=
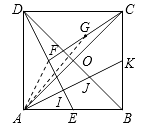
②正确，连接EO并延长，交CD于点L，则EL=2，由勾股定理DE=
=
∵Rt△EOH∽Rt△EDL
∴
， ∴
∴OH=
③错误，
∵AI⊥DE，∴∠ADE+∠DAI=90°
∵∠BAK+∠DAI=90°，∴∠BAK=∠ADE
∵∠KBA=∠EAD=90°，BA=AD
∴△BAK≌△ADE，∴BK=AE
∵点E是AB边的中点，∴AE=BE
∴BK=AE=BE=AB≠AK.
④正确，AB=2，则BK=BE=AE=1，AK=DE=
由△BKJ∽△DAJ，得JK=
AK=
由△IAE∽△BAK，得AI=
， ∴IK=
∴IKJK==1=BK2 ， 即
，
又∠BKI=∠JKB，∴△BKI∽△KJB
∴∠BIK=∠JBK=45°
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
阅读快车系列答案
【题目】去年6月某日自治区部分市、县的最高气温（℃）如下表：
区县 | 吐鲁番 | 塔城 | 和田 | 伊宁 | 库尔勒 | 阿克苏 | 昌吉 | 呼图壁 | 鄯善 | 哈密 |
气温（℃） | 33 | 32 | 32 | 30 | 30 | 29 | 29 | 31 | 30 | 28 |
则这10个市、县该日最高气温的众数和中位数分别是（ ）
A.32，32
B.32，30
C.30，30
D.30，32
【题目】红岭中学在“五四青年节”组织九年级全体学生320人进行了一次“爱我中华”竞赛，赛后随机抽取了部分学生成绩进行统计，制作如下频数分布表和频数分布直方图，请根据图表提供的信息，解答下列问题：
分数段（x表示分数） | 频数 | 频率 |
50≤x＜60 | 4 | 0.1 |
60≤x＜70 | 8 | b |
70≤x＜80 | a | 0.3 |
80≤x＜90 | 10 | 0.25 |
90≤x＜100 | 6 | 0.15 |
（1）表中a＝ ， b＝ ， 并补全直方图．
（2）若用扇形统计图描述此成绩分布情况，则分数段60≤x＜70对应扇形的圆心角度数是；
（3）请估计该年级分数在80≤x＜100的学生有多少人？
