��Ŀ����
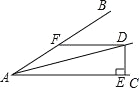
����Ŀ����ͼ��������ֱ�����dzߵ�60��Ǻ�90��ǵĶ���A������һ�𣮽����dz�ADE�Ƶ�A��ת����ת���������dz�ADE�ı�ADʼ���ڡ�BAC���ڲ�����ת�����У�̽����
��1����BAE���CAD�Ķ����к�������ϵ����˵�����ɣ�
��2����˵����CAE����BAD��30�㣻
��3������BAD�͡�CAE��ƽ����AM��AN������ת�����С�MAN��ֵ�Ƿ����仯�������䣬����������ֵ�����仯��������仯��Χ��
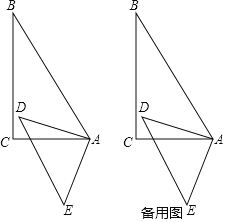
���𰸡���1����BAE+��CAD��150�㣬���ɼ���������2������������3������ת�����С�MAN��ֵ���ᷢ���仯����MAN��75�㣮
��������
��1����������õ���BAD+��CAD��60�㣬��CAE+��CAD��90�㣬���ݽǵĺͲ�ɵõ�������
��2����������õ���BAD+��CAD��60�㣬��CAE+��CAD��90�㣬�з��̼��ɵõ�������
��3����������õ���BAD+��CAD��60�㣬��CAE+��CAD��90�㣬���ݽ�ƽ���ߵĶ���ͽǵĺͲ�ɵõ�������
��1����BAE+��CAD��150�㣮����������
�ߡ�BAD+��CAD��60�㣬��CAE+��CAD��90�㣬���BAE����BAD+��CAD+��CAE��60��+90�㩁��CAD�����BAE+��CAD��150�㣻
��2���ߡ�BAD+��CAD��60�㣬��CAE+��CAD��90�㣬���CAD��60�㩁��BAD����CAD��90�㩁��CAE����60�㩁��BAD��90�㩁��CAE�����CAE����BAD��90�㩁60�㣽30�㣻
��3������ת�����С�MAN��ֵ���ᷢ���仯������������
��ͼ������BAD+��CAD��60�㣬��CAE+��CAD��90�㣬���BAD��60�㩁��CAD����CAE��90�㩁��CAD��
��AM��AN�ֱ��ǡϡ�BAD�͡�CAE��ƽ���������MAD![]() ��BAD��30��
��BAD��30��![]() ��CAD����NAC
��CAD����NAC![]() ��CAE��45��
��CAE��45��![]() ��CAD��
��CAD��
�ߡ�MAN����MAD+��CAD+��NAC��30��![]() ��CAD+��CAD+45��
��CAD+��CAD+45��![]() ��CAD��75�㣮
��CAD��75�㣮

 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д� ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д�