Question

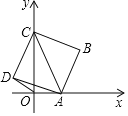
【题目】如图，点A是x轴上的一个动点，点C在y轴上，以AC为对角线画正方形ABCD，已知点C的坐标是，设点A的坐标为．

当时，正方形ABCD的边长______．

连结OD，当时，______．

Answer 1

【答案】；2或6

【解析】

(1)在RtAOC中，利用勾股定理求出AC的长度，然后再求得正方形的边长即可；

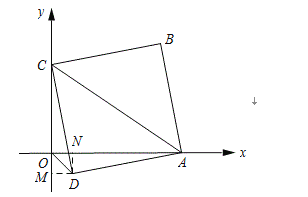
（2）先求得OD与y轴的夹角为45，然后依据OD的长，可求得点D的坐标，过D作DM⊥y轴，DN⊥x轴，接下来，再证明△DNA≌△DMC,从而可得到CM=AM,从而可得到点A的坐标.

解：（1）当n=2时，OA=2,

在Rt△COA中,AC2=CO2+AO2=20,

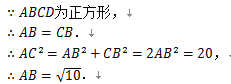
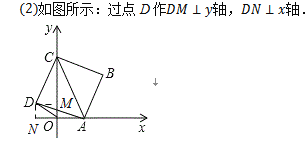
如图所示，作DM⊥y轴，DN⊥x轴，

故答案为：(1). ； (2). 2或6