Question

【题目】如图，将8个边长为1的小正方形叠放，过其四个角的顶点A、E、F、G作一个矩形ABCD，则矩形ABCD的面积为__________.

Answer 1

【答案】

【解析】

根据矩形、正方形的性质可以证得，，设，，则可求得，，根据，求得，所以，从而求得矩形的面积．

如图，

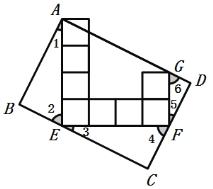
∵四边形ABCD是矩形，AE、EF、FG是8个小正方形组成的图形的边，

∴∠C=∠D =∠EFG=，

∴∠3+∠4=∠5+∠6=∠4+∠5=，

∴∠3=∠5，

∴，

∴，

设，，则，，

∵四边形ABCD是矩形，AE、EF、FG是正方形的边，

∴∠B=∠C=∠AEF =，

∴∠1+∠2=∠3+∠4=∠2+∠3=，

∴∠1=∠3，

，∠B=∠C=，

∴，

∴，，

∵四边形ABCD是矩形，

∴，

∴，

∴，

在中，∠C=，，，，

∴，

∴，

∴，

矩形ABCD的面积为：

．

故答案为：．