ЬтФПФкШн
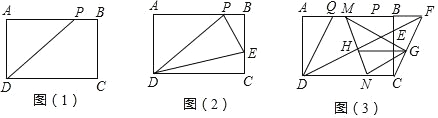
ЁОЬтФПЁПдкбЇЯАСЫОиаЮетНкФкШнжЎКѓЃЌУїУїЭЌбЇЗЂЯжЩњЛюжаЕФКмЖрОиаЮЖМКмЬиЪтЃЌШчЮвУЧЕФПЮБОЗтУцЁЂA4 ЕФДђгЁжНЕШЃЌетаЉОиаЮЕФГЄгыПэжЎБШЖМЮЊ![]() ЃК1ЃЌЮвУЧНЋОпгаетРрЬиеїЕФОиаЮГЦЮЊЁАЭъУРОиаЮЁБШчЭМЃЈ1ЃЉЃЌдкЁАЭъУРОиаЮЁБABCD жаЃЌЕу P ЮЊ AB БпЩЯЕФЖЈЕуЃЌЧв APЃНADЃЎ
ЃК1ЃЌЮвУЧНЋОпгаетРрЬиеїЕФОиаЮГЦЮЊЁАЭъУРОиаЮЁБШчЭМЃЈ1ЃЉЃЌдкЁАЭъУРОиаЮЁБABCD жаЃЌЕу P ЮЊ AB БпЩЯЕФЖЈЕуЃЌЧв APЃНADЃЎ
ЃЈ1ЃЉЧѓжЄЃКPDЃНABЃЎ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌШєдкЁАЭъУРОиаЮЁАABCD ЕФБп BC ЩЯгавЛЖЏЕу EЃЌЕБ![]() ЕФжЕЪЧЖрЩйЪБЃЌЁїPDE ЕФжмГЄзюаЁЃП
ЕФжЕЪЧЖрЩйЪБЃЌЁїPDE ЕФжмГЄзюаЁЃП
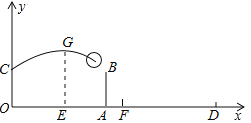
ЃЈ3ЃЉШчЭМЃЈ3ЃЉЃЌЕу Q ЪЧБп AB ЩЯЕФЖЈЕуЃЌЧв BQЃНBCЃЎвбжЊ ADЃН1ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТСЌНг DE ВЂбгГЄНЛ AB ЕФбгГЄЯпгкЕу FЃЌСЌНг CFЃЌG ЮЊ CF ЕФжаЕуЃЌMЁЂN ЗжБ№ЮЊЯпЖЮ QF КЭ CD ЩЯЕФЖЏЕуЃЌЧвЪМжеБЃГж QMЃНCNЃЌMN гы DF ЯрНЛгкЕу HЃЌЧыЮЪ GH ЕФГЄЖШЪЧЖЈжЕТ№ЃПШєЪЧЃЌЧыЧѓГіЫќЕФжЕЃЌШєВЛЪЧЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЈ2ЃЉ![]() ЃЈ3ЃЉ
ЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтжаЁАЭъУРОиаЮЁБЕФЖЈвхЩшГіADгыABЃЌИљОнAP=ADЃЌРћгУЙДЙЩЖЈРэБэЪОГіPDЃЌМДПЩЕУжЄЃЛ
ЃЈ2ЃЉШчЭМЃЌзїЕуPЙигкBCЕФЖдГЦЕуPЁфЃЌСЌНгDPЁфНЛBCгкЕуEЃЌДЫЪБЁїPDEЕФжмГЄзюаЁЃЌЩшAD=PA=BC=aЃЌБэЪОГіABгыCDЃЌгЩAB-APБэЪОГіBPЃЌгЩЖдГЦЕФаджЪЕУЕНBP=BPЁфЃЌгЩЦНааЕУБШР§ЃЌЧѓГіЫљЧѓБШжЕМДПЩЃЛ
ЃЈ3ЃЉGH=![]() ЃЌРэгЩЮЊЃКгЩЃЈ2ЃЉПЩжЊBF=BP=AB-APЃЌгЩЕШЪНЕФаджЪЕУЕНMF=DNЃЌРћгУAASЕУЕНЁїMFHЁеЁїNDHЃЌРћгУШЋЕШШ§НЧаЮЖдгІБпЯрЕШЕУЕНFH=DHЃЌдйгЩGЮЊCFжаЕуЃЌЕУЕНHGЮЊжаЮЛЯпЃЌРћгУжаЮЛЯпаджЪЧѓГіGHЕФГЄМДПЩЃЎ
ЃЌРэгЩЮЊЃКгЩЃЈ2ЃЉПЩжЊBF=BP=AB-APЃЌгЩЕШЪНЕФаджЪЕУЕНMF=DNЃЌРћгУAASЕУЕНЁїMFHЁеЁїNDHЃЌРћгУШЋЕШШ§НЧаЮЖдгІБпЯрЕШЕУЕНFH=DHЃЌдйгЩGЮЊCFжаЕуЃЌЕУЕНHGЮЊжаЮЛЯпЃЌРћгУжаЮЛЯпаджЪЧѓГіGHЕФГЄМДПЩЃЎ
ЃЈ1ЃЉдкЭМ1жаЃЌЩшAD=BC=aЃЌдђгаAB=CD=![]() aЃЌ
aЃЌ
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯA=90ЁуЃЌ
ЁпPA=AD=BC=aЃЌ
ЁрPD=![]() =
=![]() aЃЌ
aЃЌ
ЁпAB=![]() aЃЌ
aЃЌ
ЁрPD=ABЃЛ
ЃЈ2ЃЉШчЭМЃЌзїЕуPЙигкBCЕФЖдГЦЕуPЁфЃЌ
СЌНгDPЁфНЛBCгкЕуEЃЌДЫЪБЁїPDEЕФжмГЄзюаЁЃЌ
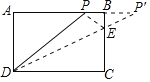
ЩшAD=PA=BC=aЃЌдђгаAB=CD=![]() aЃЌ
aЃЌ
ЁпBP=AB-PAЃЌ
ЁрBPЁф=BP=![]() a-aЃЌ
a-aЃЌ
ЁпBPЁфЁЮCDЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ3ЃЉGH=![]() ЃЌРэгЩЮЊЃК
ЃЌРэгЩЮЊЃК
гЩЃЈ2ЃЉПЩжЊBF=BP=AB-APЃЌ
ЁпAP=ADЃЌ
ЁрBF=AB-ADЃЌ
ЁпBQ=BCЃЌ
ЁрAQ=AB-BQ=AB-BCЃЌ
ЁпBC=ADЃЌ
ЁрAQ=AB-ADЃЌ
ЁрBF=AQЃЌ
ЁрQF=BQ+BF=BQ+AQ=ABЃЌ
ЁпAB=CDЃЌ
ЁрQF=CDЃЌ
ЁпQM=CNЃЌ
ЁрQF-QM=CD-CNЃЌМДMF=DNЃЌ
ЁпMFЁЮDNЃЌ
ЁрЁЯNFH=ЁЯNDHЃЌ
дкЁїMFHКЭЁїNDHжаЃЌ
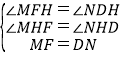 ЃЌ
ЃЌ
ЁрЁїMFHЁеЁїNDHЃЈAASЃЉЃЌ
ЁрFH=DHЃЌ
ЁпGЮЊCFЕФжаЕуЃЌ
ЁрGHЪЧЁїCFDЕФжаЮЛЯпЃЌ
ЁрGH=![]() CD=
CD=![]()
![]() ЁС2=
ЁС2=![]() ЃЎ
ЃЎ