题目内容
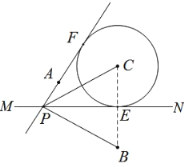
【题目】如图,AB是⊙O的直径, BC交⊙O于点D,E是![]() 的中点,连接AE交BC于点F,∠ACB =2∠EAB.
的中点,连接AE交BC于点F,∠ACB =2∠EAB.
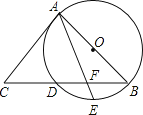
(1)求证:AC是⊙O的切线;
(2)若![]() ,
,![]() ,求BF的长.
,求BF的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接AD,如图,根据圆周角定理,再根据切线的判定定理得到AC是⊙O的切线;
(2)作F做FH⊥AB于点H,利用余弦定义,再根据三角函数定义求解即可
(1)证明:如图,连接AD.
∵ E是![]() 中点,
中点,
∴![]() .
.
∴ ∠DAE=∠EAB.
∵ ∠C =2∠EAB,
∴∠C =∠BAD.
∵ AB是⊙O的直径.
∴ ∠ADB=∠ADC=90°.
∴ ∠C+∠CAD=90°.
∴ ∠BAD+∠CAD=90°.
即 BA⊥AC
∴ AC是⊙O的切线.
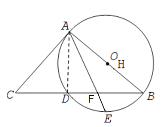
(2)解:如图②,过点F做FH⊥AB于点H.
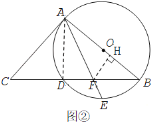
∵ AD⊥BD,∠DAE=∠EAB,
∴ FH=FD,且FH∥AC.
在Rt△ADC中,
∵![]() ,
,![]() ,
,
∴ CD=6.
同理,在Rt△BAC中,可求得BC=![]() .
.
∴BD= ![]() .
.
设 DF=x,则FH=x,BF=![]() -x.
-x.
∵ FH∥AC,
∴ ∠BFH=∠C.
∴![]() .
.
即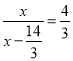 .
.
解得x=2.
∴BF=![]() .
.

练习册系列答案
相关题目
【题目】已知:点A、点B在直线![]() 的两侧.
的两侧.
(点A到直线![]() 的距离小于点B到直线
的距离小于点B到直线![]() 的距离).
的距离).
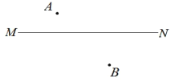
如图, (1)作点B关于直线 (2)以点C为圆心, (3)过点A作 (4)连接 |
|
根据以上作图过程及所作图形,下列四个结论中:
①![]() 是
是![]() 的切线; ②
的切线; ②![]() 平分
平分![]() ;
;
③![]() ; ④
; ④![]() .
.
所有正确结论的序号是___________________________.