题目内容
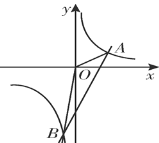
【题目】如图，反比例函数y1=
的图象与直线y2＝3x－5相交于A(2，m)，B(n，－6)两点.
(1)求反比例函数的表达式；
(2) 当y1﹥y2﹥0时，请直接写出x的取值范围；
(3)连接OA，OB，求△AOB的面积．
【答案】（1）y1=
；（2）0＜x＜2；（3）
.
【解析】
（1）根据直线和双曲线的交点坐标即可求解；
（2）观察反比例函数图象在一次函数图象上方且在x轴的上方的x的取值范围便可；
（3）根据直线与y轴的交点，根据三角形面积公式即可求解．
（1）将A(2，m)，B(n，－6)代入y2＝3x－5得：
，
，
解得：
，
，
∴点A的坐标为：(2，1)，点B的坐标为 (
，－6) ，
将A(2，1)代入y1=
得
，
，
所以反比例函数的表达式为：y1=；
(2) ∵点A的坐标为：(2，1)，
∴由图象可知，当y1﹥y2﹥0时，x的取值范围是：0＜x＜2；
(3) 设直线
与y轴交于C，
当
时，
，
即
，
∴
∴
练习册系列答案
相关题目
