题目内容
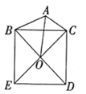
【题目】如图，在
中，
，
，以
为边在外作正方形
，
、
交于点
，则线段
的最大值为_______．
【答案】
【解析】
过O作OF⊥AO且使OF=AO，连接AF、CF，可知△AOF是等腰直角三角形，进而可得AF=
AO，根据正方形的性质可得OB=OC，∠BOC=90°，进而可得∠AOB=∠COF，进而可得△AOB≌△COF，即可证明AB=CF，当点A、C、F三点不共线时，根据三角形的三边关系可得AC+CF>AF，当点A、C、F三点共线时可得AC+CF=AC+AB=AF=6，即可得AF的最大值，由AF=AO即可得答案．
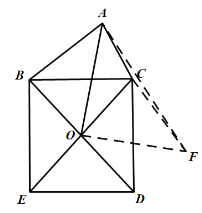
如图，过O作OF⊥AO且使OF=AO，连接AF、CF，
∴∠AOF=90°，△AOF是等腰直角三角形，
∴AF=AO，
∵四边形BCDE是正方形，
∴OB=OC，∠BOC=90°，
∵∠BOC=∠AOF=90°，
∴∠AOB+∠AOC=∠COF+∠AOC，
∴∠AOB=∠COF，
又∵OB=OC，AO=OF，
∴△AOB≌△COF，
∴CF=AB=4，
当点A、C、F三点不共线时，AC+CF>AF，
当点A、C、F三点共线时，AC+CF=AC+AB=AF=6，
∴AF≤AC+CF=6，
∴AF的最大值是6，
∴AF=AO=6，
∴AO=
．
故答案为：
练习册系列答案
相关题目
