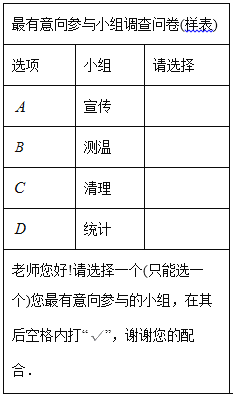
题目内容
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴的交点坐标为
轴的交点坐标为![]() 和
和![]() .
.
(1)求![]() 和
和![]() (用
(用![]() 的代数式表示);
的代数式表示);
(2)若在自变量![]() 的值满足
的值满足![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 的最大值为1,求
的最大值为1,求![]() 的值;
的值;
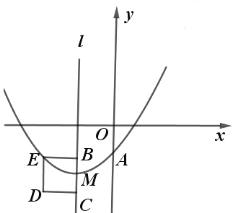
(3)已知点![]() 和点
和点![]() .若二次函数
.若二次函数![]() 的图象与线段
的图象与线段![]() 有两个不同的交点,直接写出
有两个不同的交点,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() 和
和![]() ;(3)
;(3)![]() 的取值范围为
的取值范围为![]() .
.
【解析】
(1)二次函数![]() 的图象与
的图象与![]() 轴的交点坐标为
轴的交点坐标为![]() 和
和![]() ,可以看成方程
,可以看成方程![]() 的两个实数根为
的两个实数根为![]() ,
,![]() ,利用根与系数的关系进行求解即可;
,利用根与系数的关系进行求解即可;
(2)二次函数图象开口向下,对称轴为![]() ,分3种情况进行讨论,当
,分3种情况进行讨论,当![]() 、
、 ![]() 、
、![]() 时, 根据二次函数的图像和性质进行求解即可;
时, 根据二次函数的图像和性质进行求解即可;
(3)取临界点,当点A,点B在二次函数![]() 上时,求出m的值,即可求得m的取值范围.
上时,求出m的值,即可求得m的取值范围.
(1)由题意可知,方程![]() 的两个实数根为
的两个实数根为![]() ,
,![]() .
.
∴![]() .
.
∵![]() .
.
(2)由题意可知,二次函数图象开口向下,顶点坐标为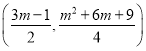 .
.
①当![]() ,即
,即![]() 时,
时,
在自变量![]() 的值满足
的值满足![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 随
随![]() 的增大而减小.
的增大而减小.
故当![]() 时,
时,![]() 为最大值.
为最大值.
∴![]() ,解得
,解得![]() 和
和![]() ,
,![]() ,
,![]() 都不合题意,舍去.
都不合题意,舍去.
②当![]() ,即
,即![]() 时,
时,![]() 为最大值,
为最大值,
∴![]() ,解得
,解得![]() ,
,![]() ,
,![]() 不合题意,舍去.
不合题意,舍去.
③当![]() ,即
,即![]() 时,
时,
在自变量![]() 的值满足
的值满足![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 随
随![]() 的增大而增大.
的增大而增大.
故当![]() 时,
时,![]() 为最大值.
为最大值.
∴![]() ,解得
,解得![]() 和
和![]() ,
,![]() 不合题意,舍去.
不合题意,舍去.
综上所述,![]() 和
和![]() .
.
(3)当点![]() 在二次函数
在二次函数![]() 上时,代入得,
上时,代入得,
![]() ,代入
,代入![]() ;
;![]() 得
得
![]() ,
,
当点![]() 在二次函数
在二次函数![]() 上时,代入得,
上时,代入得,
![]() ,代入
,代入![]() ;
;![]() 得
得
![]() ,
,
∵二次函数![]() 的图象与线段
的图象与线段![]() 有两个不同的交点
有两个不同的交点
∴![]() .
.

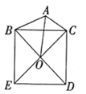
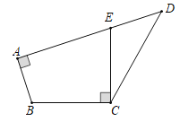
【题目】如图,ABCD中,∠A=45°,连接BD,且BD⊥AD,点E、点F分别是AB、CD上的点,连接EF交BD于点O,且EF⊥CD,BE=DF=1.
(1)求EF的长;
(2)直接写出ABCD的面积 .

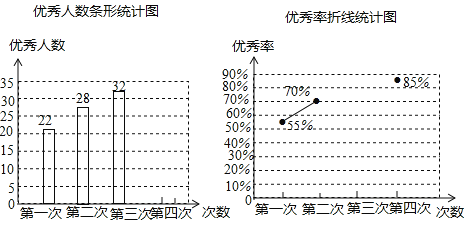
【题目】![]() 年,我省中考体育分值增加到
年,我省中考体育分值增加到![]() 分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
成绩 |
|
|
|
|
|
等级 |
|
|
|
|
|
百分比 |
|
|
|
|
|
(1)求样本容量及表格中的![]() 和
和![]() 的值
的值
(2)求扇形统计图中![]() 等级所对的圆心角度数,并补全统计图.
等级所对的圆心角度数,并补全统计图.
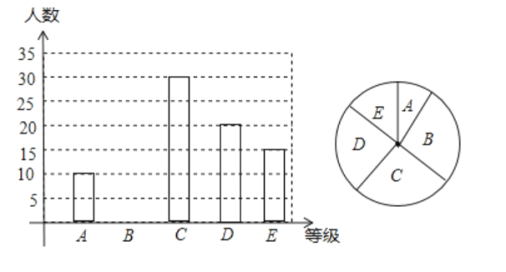
(3)我校![]() 年级共有女生
年级共有女生![]() 人.若女生八百米成绩的达标成绩为
人.若女生八百米成绩的达标成绩为![]() 分,我校九年级女生八百米成绩达标的人数有多少?
分,我校九年级女生八百米成绩达标的人数有多少?