题目内容
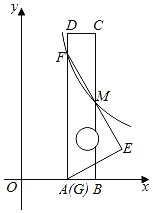
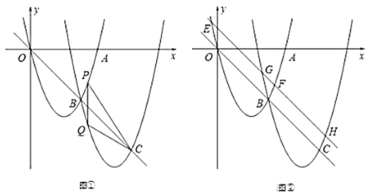
【题目】如图①,抛物线![]() 交
交![]() 正半轴于点
正半轴于点![]() ,将抛物线
,将抛物线![]() 先向右平移
先向右平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位得到抛物线
个单位得到抛物线![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
(1)求抛物线![]() 的解析式;
的解析式;
(2)点![]() 是抛物线
是抛物线![]() 上
上![]() (含端点)间的一点,作
(含端点)间的一点,作![]() 轴交抛物线
轴交抛物线![]() 于点
于点![]() ,连按
,连按![]() ,
,![]() .当
.当![]() 的面积为
的面积为![]() 时, 求点
时, 求点![]() 的坐标;
的坐标;
(3)如图②,将直线![]() 向上平移,交抛物线
向上平移,交抛物线![]() 于点
于点![]() 、
、![]() ,交抛物线
,交抛物线![]() 于点
于点![]() 、
、![]() ,试判断
,试判断![]() 的值是否为定值,并说明理由.
的值是否为定值,并说明理由.
【答案】(1)![]() ;(2)点
;(2)点![]() 的坐标为(4,0)或(5,5);(3)
的坐标为(4,0)或(5,5);(3)![]() 的值的定值
的值的定值![]() ,理由见解析.
,理由见解析.
【解析】
(1)先将抛物线M1:y=x2-4x化为顶点式,由平移规律“上加下减,左加右减”可直接写出抛物线M2的解析式;
(2) 分别求出点A,点B,点C的坐标,求出m的取值范围,再用含m的代数式表示出△CPQ的面积,可用函数的思想求出其最大值;
(3) 设将直线OB向上平移k个单位长度得到直线EH,分别求出点E,F,G,H的横坐标,分别过G,H作y轴的平行线,过E,F作x轴的平行线,构造全等三角形△GEM与△HFN,可通过全等三角形的性质求出![]() 的值为定值1.
的值为定值1.
(1)![]()
![]() 将其先向右平移
将其先向右平移![]() 个单位,再向上平移3个单位的解析式为:
个单位,再向上平移3个单位的解析式为:
![]()
(2)![]() 抛物线
抛物线![]() 与
与![]() 交于点
交于点![]()
![]()
解得,![]()
![]()
将点![]() 代入
代入![]()
得,![]()
![]()
![]() 抛物线
抛物线![]() 与直线
与直线![]() 交于点
交于点![]()
![]()
解得,![]() ,
,![]() ,
,
![]()
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,
,
![]()
![]()
即:![]()
解得:![]() ,
,![]()
在![]() 中
中
当![]() 时,
时,![]() ,
,![]() ,
,
![]()
![]()
![]()
![]() 在
在![]() 中
中
根据二次函数的图象及性质可知
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]()
(3)![]() 的值的定值
的值的定值![]() ,理由如下:
,理由如下:
设直线![]() 向下平移
向下平移![]() 个单位长度得到直线
个单位长度得到直线![]()
则![]()
令![]()
解得,![]() ,
,![]()
![]() ,
,![]()
令![]()
解得,![]() ,
,![]()
![]() ,
,![]()
![]()
![]()
分别过![]() ,
,![]() 作
作![]() 轴的平行线,过
轴的平行线,过![]() ,
,![]() 作
作![]() 轴的平行线,交点分别为
轴的平行线,交点分别为![]() ,
,![]() ,
,![]() ,如下图所示:
,如下图所示:
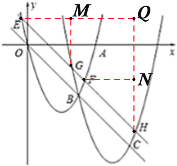
则![]() ,
,![]()
![]()
![]()
![]()
![]() 的值的定值是
的值的定值是![]()

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
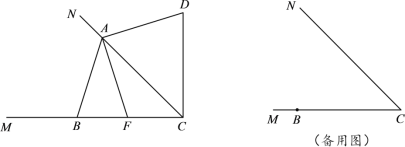
英才计划期末调研系列答案【题目】如图,ABCD中,∠A=45°,连接BD,且BD⊥AD,点E、点F分别是AB、CD上的点,连接EF交BD于点O,且EF⊥CD,BE=DF=1.
(1)求EF的长;
(2)直接写出ABCD的面积 .

【题目】某年级共有150名女生,为了解该校女生实心球成绩(单位:米)和仰卧起坐(单位:个)的情况,从中随机抽取30名女生进行测试,获得了她们的相关成绩,并对数据进行整理、描述和分析,下面给出了部分信息.
![]() .实心球成绩的频数分布表如下:
.实心球成绩的频数分布表如下:
分组 | 6.2≤ | 6.6≤ | 7.0≤ | 7.4≤ | 7.8≤ | 8.2≤ |
频数 | 2 |
| 10 | 6 | 2 | 1 |
![]() .实心球成绩在7.0≤
.实心球成绩在7.0≤![]() <7.4.这组的是:
<7.4.这组的是:
7.0 | 7.0 | 7.0 | 7.1 7.1 | 7.1 | 7.2 | 7.2 | 7.3 | 7.3 |
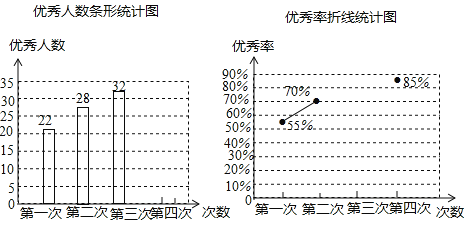
![]() .一分钟仰卧起坐成绩如图所示:
.一分钟仰卧起坐成绩如图所示:

根据以上信息,回答下列问题:
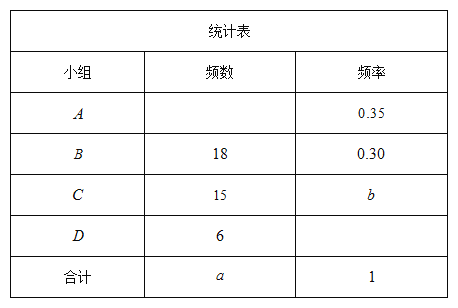
(1)①表中m的值为 ;
②抽取学生一分钟仰卧起坐成绩的中位数为 个;
(2)若实心球成绩达到7.2米及以上,成绩记为优秀,请估计全年级女生成绩达到优秀的人数.
(3)该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下:
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有2名女生的一分钟仰卧起坐成绩未抄录完整,当老师说这8名女生恰好有4人两项测试成绩都达到了优秀,于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀,你同意体育委员的说法吗?并说明你的理由.