题目内容
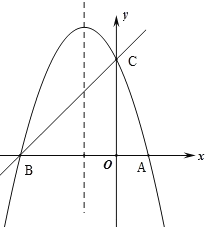
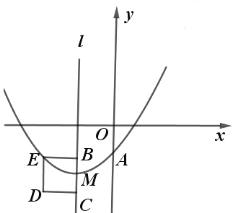
【题目】如图，抛物线
与
轴交于点
，与
轴的交点
在点
与点
之间（不包括这两点），对称轴为直线
．有下列结论：
①
；②
；③
；④若点
，
在抛物线上，则
．其中正确结论的个数是（）
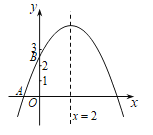
A.
B.
C.
D.
【答案】C
【解析】
①先根据抛物线的开口方向、与y轴的交点可求出a、c的符号与取值范围，再根据对称轴可求出b的符号即可；②先根据对称性可知抛物线与x轴的另一个交点为
，从而可得当
时，
，再结合
即可得；③将点
代入可得一个关于a、b、c的等式，再结合对称轴和c的取值范围即可得；④先求出
和
的取值范围，再求出点N在抛物线上的对称点
的横坐标
的取值范围，然后利用二次函数的增减性分析即可得．
抛物线的开口向下，且与y轴的交点B在点
与点
之间（不包括这两点）
，
对称轴为
，则结论①正确
由二次函数的对称性可知，抛物线与x轴的另一个交点为
则当时，
即
，即
，则结论②正确
将点代入抛物线得：
，即
又
解得
，则结论③正确
，
由结论③可知，
，
由对称性可知，当
时，
由二次函数的性质可知，当
时，y随x的增大而减小
虽然和均大于2，但它们的大小关系不能确定
所以
与
的大小不能确定，则结论④错误
综上，正确结论的个数是3个
故选：C．
【题目】某年级共有150名女生，为了解该校女生实心球成绩（单位：米）和仰卧起坐（单位：个）的情况，从中随机抽取30名女生进行测试，获得了她们的相关成绩，并对数据进行整理、描述和分析，下面给出了部分信息．
．实心球成绩的频数分布表如下：
分组 | 6．2≤ | 6．6≤ | 7．0≤ | 7．4≤ | 7．8≤ | 8．2≤ |
频数 | 2 |
| 10 | 6 | 2 | 1 |
．实心球成绩在7．0≤
＜7．4．这组的是：
7.0 | 7.0 | 7.0 | 7.1 7.1 | 7.1 | 7.2 | 7.2 | 7.3 | 7.3 |
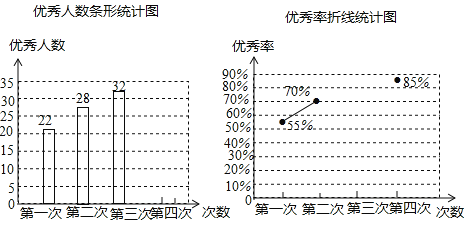
．一分钟仰卧起坐成绩如图所示：
根据以上信息，回答下列问题：
（1）①表中m的值为 ；
②抽取学生一分钟仰卧起坐成绩的中位数为 个；
（2）若实心球成绩达到7．2米及以上，成绩记为优秀，请估计全年级女生成绩达到优秀的人数．
（3）该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下：
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8．1 | 7．7 | 7．5 | 7．5 | 7．3 | 7．2 | 7．0 | 6．5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有2名女生的一分钟仰卧起坐成绩未抄录完整，当老师说这8名女生恰好有4人两项测试成绩都达到了优秀，于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀，你同意体育委员的说法吗？并说明你的理由．
