题目内容
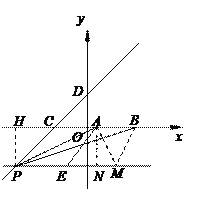
【题目】已知抛物线y=ax2+bx+5与x轴交于点A(1,0)和点B(5,0),顶点为M.点C在x轴的负半轴上,且AC=AB,点D的坐标为(0,3),直线l经过点C、D.
(1)求抛物线的表达式;
(2)点P是直线l在第三象限上的点,联结AP,且线段CP是线段CA、CB的比例中项,
求tan∠CPA的值;
(3)在(2)的条件下,联结AM、BM,在直线PM上是否存在点E,使得∠AEM=∠AMB.若存在,求出点E的坐标;若不存在,请说明理由.
【答案】 (1)![]() ;(2)
;(2) ![]() ;(3)E的坐标为(-2,-4)或(4,-4).
;(3)E的坐标为(-2,-4)或(4,-4).
【解析】试题分析:(1)把A、B两点带入抛物线解析式,求得a、b的值,即可得到抛物线解析式;
(2)由AC=AB且点C在点A的左侧,及线段CP是线段CA、CB的比例中项,可得CP=![]() ,
,
由两边对应成比例且夹角相等的三角形相似,可得△CPA∽△CBP,由此∠CPA= ∠CBP.
过P作PH⊥x轴于H,易得PH=4,H(-7,0),BH=12. 由于P(-7,-4),可求![]() ;
;
(3)分两种情况:点E在M左侧和点E在M右侧讨论即可.
试题解析:(1)∵ 抛物线![]() 与x轴交于点A(1,0),B(5,0),
与x轴交于点A(1,0),B(5,0),
∴![]() ,
,
解得![]()
∴ 抛物线的解析式为![]() .
.
(2)∵ A(1,0),B(5,0),
∴ OA=1,AB=4.
∵ AC=AB且点C在点A的左侧,
∴ AC=4 .
∴ CB=CA+AB=8.
∵ 线段CP是线段CA、CB的比例中项,
∴ ![]() .
.
∴ CP=![]() .
.
又 ∵ ∠PCB是公共角,
∴ △CPA∽△CBP .
∴ ∠CPA= ∠CBP.
过P作PH⊥x轴于H.
∵ OC=OD=3,∠DOC=90°,
∴ ∠DCO=45°.∴ ∠PCH=45°
∴ PH=CH=CP![]() =4,
=4,
∴ H(-7,0),BH=12,
∴ P(-7,-4),
∴![]() ,
,
tan∠CPA=![]() .
.
(3) ∵ 抛物线的顶点是M(3,-4),
又 ∵ P(-7,-4),
∴ PM∥x轴 .
当点E在M左, 则∠BAM=∠AME.
∵ ∠AEM=∠AMB,
∴ △AEM∽△BMA.
∴![]() ,
,
∴![]() .
.
∴ ME=5,∴ E(-2,-4).
过点A作AN⊥PM于点N,则N(1,-4).
当点E在M右侧时,记为点![]() ,
,
∵ ∠A![]() N=∠AEN,
N=∠AEN,
∴ 点![]() 与E 关于直线AN对称,则
与E 关于直线AN对称,则![]() (4,-4).
(4,-4).
综上所述,E的坐标为(-2,-4)或(4,-4).