题目内容
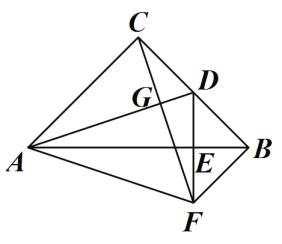
【题目】如图，在△ABC中，tanA=
，∠B=45°，AB=14. 求BC的长.
【答案】∴BC=6
【解析】试题分析：
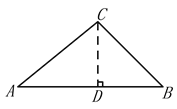
如图，过点C作CD⊥AB于点D，得到Rt△ADC和Rt△BCD，由在Rt△ADC中tanA=
，设CD=3x，AD=4x，则在Rt△BCD中，由∠B=45°，可得BD=CD=3x，结合AB=14由勾股定理列出方程解得x的值，再在Rt△BCD中，由勾股定理即可求得BC的值.
试题解析：
如图，过点C作CD⊥AB于点D，
∴∠ADC=∠BDC=90°，
∵tanA=
，
∴
，
设CD=3x，则AD=4x，
∵∠B=45°，∠BDC=90°，
∴BD=CD=3x，
∵AD+BD=AB=14，
∴4x+3x=14，解得x=2，
∴BD=CD=6，
∴BC=
.
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
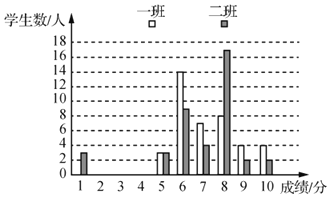
【题目】8年级某老师对一、二班学生阅读水平进行测试，并将成绩进行了统计，绘制了如下图表(得分为整数，满分为10分，成绩大于或等于6分为合格，成绩大于或等于9分为优秀)．
平均分 | 方差 | 中位数 | 众数 | 合格率 | 优秀率 | |
一班 | 7.2 | 2.11 | 7 | 6 | 92.5% | 20% |
二班 | 6.85 | 4.28 | 8 | 8 | 85% | 10% |
根据图表信息，回答问题：
(1)用方差推断， 班的成绩波动较大；用优秀率和合格率推断， 班的阅读水平更好些；
(2)甲同学用平均分推断，一班阅读水平更好些；乙同学用中位数或众数推断，二班阅读水平更好些．你认为谁的推断比较科学合理，更客观些．为什么？