题目内容
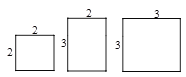
【题目】有5张边长为2的正方形纸片，4张边长分别为2、3的矩形纸片，6张边长为3的正方形纸片，从其中取出若干张纸片，且每种纸片至少取一张，把取出的这些纸片拼成一个正方形（原纸张进行无空隙、无重叠拼接），则拼成正方形的边长最大为 （ ）
A. 6B. 7C. 8D. 9
【答案】C
【解析】
设2为a，3为b，则根据5张边长为2的正方形纸片的面积是5a2，4张边长分别为2、3的矩形纸片的面积是4ab，6张边长为3的正方形纸片的面积是6a2，得出a2+4ab+4b2=（a+2b）2，再根据正方形的面积公式将a、b代入，即可得出答案．
解：
设2为a，3为b，
则根据5张边长为2的正方形纸片的面积是5a2，
4张边长分别为2、3的矩形纸片的面积是4ab，
6张边长为3的正方形纸片的面积是6a2，
∵a2+4ab+4b2=（a+2b）2，（b＞a）
∴拼成的正方形的边长最长可以为a+2b=2+6=8，
故选：C．
练习册系列答案
阅读快车系列答案
相关题目
