题目内容
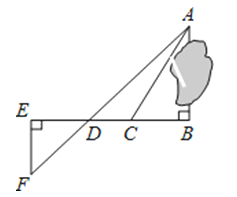
【题目】已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.
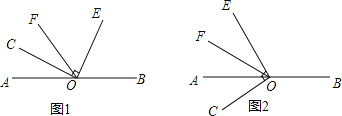
(1)如图1,若∠COF=34°,则∠BOE=______;
(2)如图1,若∠BOE=80°,则∠COF=______;
(3)若∠COF=m°,则∠BOE=______度;∠BOE与∠COF的数量关系为______.
(4)当∠COE绕点O逆时针旋转到如图2的位置时,(3)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
【答案】(1)68° (2) 40° (3) 2m ∠BOE=2∠COF;(4)成立,理由见解析.
【解析】
(1)根据互余得到∠EOF=90°-34°,再由OF平分∠AOE,得到∠AOE=2∠EOF,然后根据邻补角的定义即可得到∠BOE;
(2)设∠COF=n°,根据互余得到∠EOF=90°-n°,再由OF平分∠AOE,得到∠AOE=2∠EOF=180°-2n°,然后根据邻补角的定义得到∠BOE=180°-(180°-2n°)=2n°=80°,于是得到结论;
(3)当∠COF=m°,根据互余得到∠EOF=90°-m°,再由OF平分∠AOE,得到∠AOE=2∠EOF=180°-2m°,然后根据邻补角的定义得到∠BOE=180°-(180°-2m°)=2m°,所以有∠BOE=2∠COF;
(4)同(3),可得到∠BOE=2∠COF.
解:(1)∵∠COE是直角,∠COF=34°,
∴∠EOF=90°-34°=56°,
∵OF平分∠AOE.
∴∠AOE=2∠EOF=112°,
∴∠BOE=180°-112°=68°;
(2)设∠COF=n°,
∴∠EOF=90°-n°,
∴∠AOE=2∠EOF=180°-2n°,
∴∠BOE=180°-(180°-2n°)=2n°=80°,
∴∠COF=40°;
(3)当∠COF=m°,
∴∠EOF=90°-m°,
∴∠AOE=2∠EOF=180°-2m°,
∴∠BOE=180°-(180°-2m°)=2m°,
∴∠BOE=2∠COF;
(4)∠BOE与∠COF的数量关系仍然成立.理由如下:
设∠COF=n°,
∵∠COE是直角,
∴∠EOF=90°-n°,
又∵OF平分∠AOE.
∴∠AOE=2∠EOF=180°-2n°,
∴∠BOE=180°-(180°-2n°)=2n°,
即∠BOE=2∠COF.
故答案为:(1)68° ;(2) 40° ;(3) 2m ,∠BOE=2∠COF ;(4)成立,理由见解析.

【题目】某商场销售某种商品,原价560元.随着不同幅度的降价(元),日销售量(件)发生相应变化,关系如图所示:

(1)根据图像完成下表
降价/元 | 5 | 10 | 15 | |
日销售量/件 | 780 | 840 | 870 |
(2)售价为560元时,日销售量为多少件.
(3)如果该商场要求日销售量为1110件,该商品应降价多少元.
(4)设该商品的售价为![]() 元,日销售量为
元,日销售量为![]() 件,求
件,求![]() 与
与![]() 之间的关系式.
之间的关系式.