题目内容
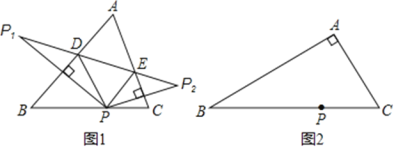
【题目】对于一个图形,通过两种不同的方法计算它们的面积,可以得到一个数学等式,例如图1可以得到
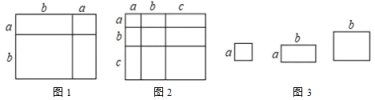
(1)类似图1的数学等式,写出图2表示的数学等式;
(2)若![]() ,
, ![]() ,用上面得到的数学等式乘
,用上面得到的数学等式乘![]() 的值;
的值;
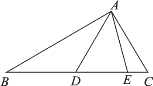
(3)小明同学用图3中的![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张边长为
张边长为![]() 的正方形,z张边长为
的正方形,z张边长为![]() 、
、![]() 的长方形拼出一个面积为
的长方形拼出一个面积为![]() 的长方形,求
的长方形,求![]() 的值.
的值.
【答案】(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)30;(3)104.
【解析】
(1)整体计算正方形的面积和分部分求和,二者相等;
(2)依据a2+b2+c2=(a+b+c)2-2ab-2ac-2bc,进行计算即可;
(3)依据所拼图形的面积为:xa2+yb2+zab,而(a+7b)(9a+4b)=9a2+67ab+28b2,可得x,y,z的值,从而得解.
解:(1)∵图2中正方形的面积有两种算法:①(a+b+c)2;②a2+b2+c2+2ab+2ac+2bc.
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
∴图2表示的数学等式:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(2)∵(a+b+c)2=a2+b2+c2+2ab+2ac+2bc,
∴a2+b2+c2=(a+b+c)2-2ab-2ac-2bc
=102-2×35
=30;
(3)由题可知,所拼图形的面积为:xa2+yb2+zab,
∵(a+7b)(9a+4b)=9a2+4ab+63ab+28b2=9a2+67ab+28b2,
∴x=9,y=28,z=67,
∴x+y+z=9+28+67=104.

【题目】探究函数y=x+![]() (x>0)与y=x+
(x>0)与y=x+![]() (x>0,a>0)的相关性质.
(x>0,a>0)的相关性质.
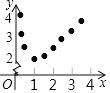
(1)小聪同学对函数y=x+![]() (x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
(x>0)进行了如下列表、描点,请你帮他完成连线的步骤;观察图象可得它的最小值为 ,它的另一条性质为 ;
x | … |
|
|
| 1 |
| 2 |
| 3 | … |
y | … |
|
|
| 2 |
|
|
|
| … |
(2)请用配方法求函数y=x+![]() (x>0)的最小值;
(x>0)的最小值;
(3)猜想函数y=x+![]() (x>0,a>0)的最小值为 .
(x>0,a>0)的最小值为 .