题目内容
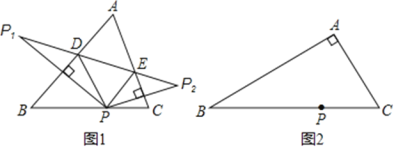
【题目】如图,在△ABC中,∠B>90°,CD为∠ACB的角平分线,在AC边上取点E,使DE=DB,且∠AED>90°.若∠A=α,∠ACB=β,则( )
A.∠AED=180°﹣α﹣βB.∠AED=180°﹣α﹣![]() β
β
C.∠AED=90°﹣α+βD.∠AED=90°+α+![]() β
β
【答案】A
【解析】
在AC上截取CF=BC,根据全等三角形的性质可得BD=DF=DE,可得∠AED=∠ABC,根据三角形的内角和可求解.
解:如图,在AC上截取CF=BC,
∵CF=BC,∠ACD=∠BCD,CD=CD,
∴△BDC≌△FDC(SAS)
∴∠ABC=∠CFD,DF=BD
∵BD=DE
∴DE=DF
∴∠DEF=∠DFE,
∴∠AED=∠CFD
∴∠AED=∠DBC=180°-∠A-∠ACB=180°-α-β
故选:A.

练习册系列答案
相关题目