题目内容
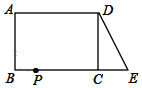
【题目】我们已经知道,有一个内角是直角的三角形是直角三角形.其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家已发现在一个直角三角形中,两个直角边边长的平方和等于斜边长的平方.如果设直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么可以用数学语言表达:a2+b2=c2.已知,如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE.
(1)DE的长为 .
(2)动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒,求当t为何值时,△ABP和△DCE全等?
(3)若动点P从点B出发,以每秒1个单位的速度仅沿着BE向终点E运动,连接DP.设点P运动的时间为t秒,是否存在t,使△PDE为等腰三角形?若存在,请直接写出t的值;否则,说明理由.
【答案】(1)5 (2)3秒或13秒 (3)t=3秒或4秒或![]() 秒
秒
【解析】
(1)根据题意可得:CD=4,根据勾股定理可求DE的长;
(2)若△ABP与△DCE全等,可得AP=CE=3或BP=CE=3,根据时间路程的关系可求r的值;
(3)分PD=DE,PE=DE,PD=PE三种情况讨论,可求t的值.
解:(1)∵四边形ABCD是矩形
∴AB=CD=4,AD=BC=6,CD⊥BC
在Rt△DCE中,DE=![]() =
=![]() =5
=5
故答案为 5.
(2)若△ABP与△DCE全等
∴BP=CE或AP=CE
当BP=CE=3时,则t=![]() =3秒
=3秒
当AP=CE=3时,则t=![]() =13秒
=13秒
∴求当t为3秒或13秒时,△ABP和△DCE全等.
(3)若△PDE为等腰三角形
则PD=DE或PE=DE或PD=PE
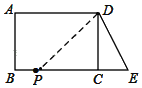
当PD=DE时,
∵PD=DE,DC⊥BE
∴PC=CE=3
∵BP=BC﹣CP=3
∴t=![]() =3
=3
当PE=DE=5时,
∵BP=BE﹣PE
∴BP=9﹣5=4
∴t=![]() =4
=4
当PD=PE时,
∴PE=PC+CE=3+PC
∴PD=3+PC
在Rt△PDC中,DP2=CD2+PC2.
∴(3+PC)2=16+PC2
∴PC=![]()
∵BP=BC﹣PC
∴BP=![]()
∴t=![]() =
=![]()
综上所述:当t=3秒或4秒或![]() 秒时,△PDE为等腰三角形.
秒时,△PDE为等腰三角形.

【题目】甲、乙两组同学进行一分钟引体向上测试,评分标准规定,做6个以上![]() 含6个
含6个![]() 为合格,做9个以上
为合格,做9个以上![]() 含9个
含9个![]() 为优秀,两组同学的测试成绩如下表:
为优秀,两组同学的测试成绩如下表:
成绩 | 4 | 5 | 6 | 7 | 8 | 9 |
甲组 | 1 | 2 | 5 | 2 | 1 | 4 |
乙组 | 1 | 1 | 4 | 5 | 2 | 2 |
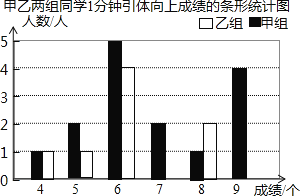
现将两组同学的测试成绩绘制成如下不完整的统计图表:
统计量 | 平均数 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲组 | a | 6 | 6 |
|
|
|
乙组 |
| b | 7 |
|
|
|
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 统计表中的
统计表中的![]() ______,
______,![]() ______;
______;
![]() 人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.
人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.